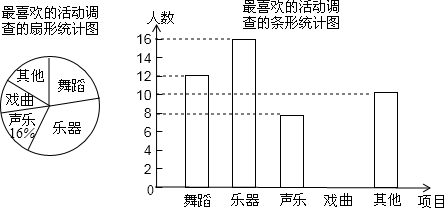
题目内容
8.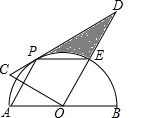 如图,在Rt△COD中,∠COD=90°,∠D=30°,斜边CD与以AB为直径,O为圆心的半圆相切于点P,OD与半圆交于点E,连接PA,PE,PA与OC交于点F.
如图,在Rt△COD中,∠COD=90°,∠D=30°,斜边CD与以AB为直径,O为圆心的半圆相切于点P,OD与半圆交于点E,连接PA,PE,PA与OC交于点F.猜想与证明:
(1)当∠BOD=60°时,试判断四边形AOEP的形状,并证明;
探索与发现:
(2)当AB=6时,求图中阴影部分的面积;
(3)若不再添加任何辅助线和字母,请写出图中两组相等的线段.(半径除外)
分析 (1)当∠BOD=60°时,四边形AOEP为菱形.连接OP,由切线的性质可知OP⊥CD,结合∠D=30°可知∠POE=60°,由∠AOP、∠POE、∠BOE三个角互补可得出∠AOP=60°,由圆的半径相等可得出△OAP与△OPE为等边三角形,结合∠PAO=60°可证出四边形AOEP为菱形;
(2)连接OP,在Rt△OPD中,由特殊角的三角形函数值可得出PD的长度,根据阴影部分的面积=△OPD的面积-扇形OPE的面积即可求出结论;
(3)在Rt△OPD中,由∠D=30°可求出OD=2OP,从而得出OD=AB;再由∠POE=60°、OP=OE可得出△OPE为等边三角形,进而得出PE=OE.
解答 解:(1)当∠BOD=60°时,四边形AOEP为菱形.
证明:连接OP,如图所示.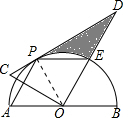
∵CD切半圆于点P,
∴OP⊥CD,
又∵∠D=30°,
∴∠DOP=60°,
又∵∠BOD=60°,
∴∠AOP=60°,
∵OE=OP=OA,
∴△OAP与△OPE为等边三角形,
∴OA=AP=PE=EO,且∠PAO=60°,
∴四边形AOEP为菱形.
(2)连接OP.
在Rt△OPD中,OP=$\frac{1}{2}$AB=3,∠OPD=90°,∠D=30°,
∴PD=$\frac{OP}{tan∠D}$=3$\sqrt{3}$,∠POE=60°,
阴影部分的面积S=$\frac{1}{2}$PD•OP-$\frac{60°}{360°}$π•OP2=$\frac{9\sqrt{3}}{2}$-$\frac{3}{2}$π.
(3)在Rt△OPD中,∠OPD=90°,∠D=30°,
∴OD=$\frac{PD}{sin∠D}$=2PD=AB,∠POE=60°.
在△OPE中,OP=OE,∠POE=60°,
∴△OPE为等边三角形,
∴PE=OE.
故可得出OD=AB,PE=OE.
点评 本题考查了切线的性质、扇形面积的计算、等边三角形的判定及性质以及角的运算,解题的关键是:(1)得出△OAP与△OPE都是等边三角形;(2)分割组合图形利用三角形面积-扇形面积得出结论;(3)解直角三角形找出边的长度.本题属于基础,难度不大,解决该题型题目时,根据边角关系找出相等的量是关键.

| A. | 38 | B. | 39 | C. | 40 | D. | 42 |
| A. |  | B. |  | C. |  | D. |  |
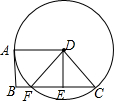 已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.
已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.