题目内容
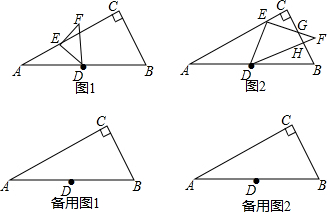
7.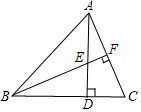 如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.
如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.(1)求证:AD=BD;
(2)若∠C=75°,求∠ABE的度数.
分析 (1)由AD是△ABC一边上的高,得到∠ADC=∠ADB=90°,根据余角 的性质得到∠DBE=∠CAD,根据全等三角形的性质即可得到AD=BD;
(2)根据等腰直角三角形的性质得到∠ABC=∠BAD=45°,由全等三角形的性质得到∠BED=∠C=75°,根据三角形的外角的性质即可得到结论.
解答 (1)证明:∵AD是△ABC一边上的高,
∴∠ADC=∠ADB=90°,
∵BF⊥AC,
∴∠BFC=90°,
∴∠C+∠CBF=∠CAD+∠C=90°,
∴∠DBE=∠CAD,
在△BDE与△ADC中,$\left\{\begin{array}{l}{∠CAD=∠DBE}\\{∠BDE=∠ADC}\\{BE=AC}\end{array}\right.$,
∴△BDE≌△ADC,
∴AD=BD;
(2)解:∵AD=BD,∠ADB=90°,
∴∠ABC=∠BAD=45°,
∵△BDE≌△ADC,
∴∠BED=∠C=75°,
∴∠ABE=30°.
点评 此题主要考查的是全等三角形的判定和性质,难度不大,找准全等的三角形是正确解决本题的关键.

练习册系列答案
相关题目
 如图,给出下列四组条件:
如图,给出下列四组条件: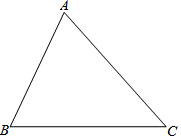 如图,在某城区地图上,有一块△ABC区域,市政规划要把△ABC区域划分成三个三角形小区域,使任何两个区域都相邻,并且使划分的三个小区域面积彼此相等.请你探究后,把符合题意的示意图画在图中,并说明所画的线是什么线.
如图,在某城区地图上,有一块△ABC区域,市政规划要把△ABC区域划分成三个三角形小区域,使任何两个区域都相邻,并且使划分的三个小区域面积彼此相等.请你探究后,把符合题意的示意图画在图中,并说明所画的线是什么线.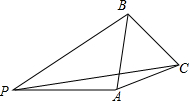 如图,P是等边三角形ABC外一点,PA=3,PB=4,PC=5,求∠BPA的度数.
如图,P是等边三角形ABC外一点,PA=3,PB=4,PC=5,求∠BPA的度数. 已知:如图,AD=BC,AB=DC,求证:∠A=∠C.
已知:如图,AD=BC,AB=DC,求证:∠A=∠C.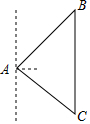 随着南海局势的升级,中国政府决定在黄岩岛填海造陆,修建机场,设立雷达塔.某日,在雷达塔A处侦测到东北方向上的点B处有一艘菲律宾渔船进入我侦测区域,且以30海里/时的速度往正南方向航行,我方与其进行多次无线电沟通无果后,这艘渔船行驶了1小时10分到达点A南偏东53°方向的C处,与此同时我方立即通知(通知时间忽略不计)与A、C在一条直线上的中国海警船往正西方向对该渔船进行侦测拦截,其中海警船位于与A相距100海里的D处.
随着南海局势的升级,中国政府决定在黄岩岛填海造陆,修建机场,设立雷达塔.某日,在雷达塔A处侦测到东北方向上的点B处有一艘菲律宾渔船进入我侦测区域,且以30海里/时的速度往正南方向航行,我方与其进行多次无线电沟通无果后,这艘渔船行驶了1小时10分到达点A南偏东53°方向的C处,与此同时我方立即通知(通知时间忽略不计)与A、C在一条直线上的中国海警船往正西方向对该渔船进行侦测拦截,其中海警船位于与A相距100海里的D处.