题目内容
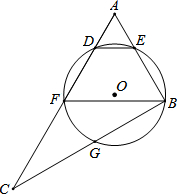 如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+
如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+
| ||
| 2 |
(1)求⊙O的半径;
(2)若DE∥BF,且AE=a,DF=2+
| 3 |
考点:点与圆的位置关系,弧长的计算
专题:
分析:(1)设⊙O的半径为r,再根据弧长公式即可得出结论;
(2)先根据DE∥BF得出∠ADE=∠AFB,再根据圆内接四边形的性质得出∠AFB+∠DEB=180°,进而得出AF的长.在Rt△ABC中,根据直角三角形的性质求出BF的长,再由B、F都在⊙O上即可得出结论.
(2)先根据DE∥BF得出∠ADE=∠AFB,再根据圆内接四边形的性质得出∠AFB+∠DEB=180°,进而得出AF的长.在Rt△ABC中,根据直角三角形的性质求出BF的长,再由B、F都在⊙O上即可得出结论.
解答:解:(1)设⊙O的半径为r,
∵∠ABC=90°
∴弧EFG所对的圆心角的度数为180°,
∴
=(1+
)π,即r=1+
;
(2)答:圆心O在直线BF上.
理由如下:
∵DE∥BF,
∴∠ADE=∠AFB.
∵四边形DEBF是⊙O的内接四边形,
∴∠AFB+∠DEB=180°.
∵∠AED+∠DEB=180°,
∴∠AFB=∠AED,
∴∠ADE=∠AED,
∴AD=AE=a.
∵DF=2+
-a,
∴AF=AD+DF=2+
.
在Rt△ABC中,∠ABC=90°且F为AC中点,
∴BF=AF=2+
.
∵r=1+
,
∴BF=2r.
∵B、F都在⊙O上,
∴BF为⊙O直径,
∴点O在直线BF上.
∵∠ABC=90°
∴弧EFG所对的圆心角的度数为180°,
∴
| 180πr |
| 180 |
| ||
| 2 |
| ||
| 2 |
(2)答:圆心O在直线BF上.
理由如下:
∵DE∥BF,
∴∠ADE=∠AFB.
∵四边形DEBF是⊙O的内接四边形,
∴∠AFB+∠DEB=180°.
∵∠AED+∠DEB=180°,
∴∠AFB=∠AED,
∴∠ADE=∠AED,
∴AD=AE=a.
∵DF=2+
| 3 |
∴AF=AD+DF=2+
| 3 |
在Rt△ABC中,∠ABC=90°且F为AC中点,
∴BF=AF=2+
| 3 |
∵r=1+
| ||
| 2 |
∴BF=2r.
∵B、F都在⊙O上,
∴BF为⊙O直径,
∴点O在直线BF上.
点评:本题考查的是点与圆的位置关系,熟知弧长公式、直角三角形的性质及圆内接四边形的性质是解答此题的关键.

练习册系列答案
相关题目
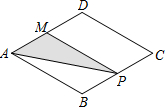 如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )



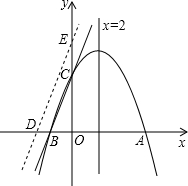 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(5,0).
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(5,0).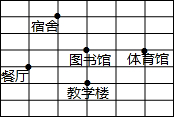 下面是某学校的平面图,请你建立直角坐标系,描述各部门的位置(写出各点的坐标即可).
下面是某学校的平面图,请你建立直角坐标系,描述各部门的位置(写出各点的坐标即可). 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:
某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数: 如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2).
如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2).