题目内容
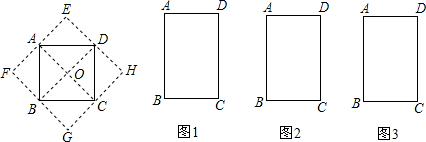
如图，正方形ABCD的两条对角线把正方形分割成四个等腰直角三角形，将这四个三角形分别沿正方形ABCD的边向外翻折，可得到一个新正方形EFGH．请你在矩形ABCD中画出分割线，将矩形分割成四个三角形，然后分别将这四个三角形沿矩形的边向外翻折，使得图1得到菱形，图2得到矩形，图3得到一般的平行四边形（只在矩形ABCD中画出分割线，说明分割线的作法，不画出翻折后的图形）．
考点：作图—应用与设计作图
专题：
分析：根据已知图形分割方法，分别利用菱形以及矩形和平行四边形的性质分别得出即可．
解答：解：如图所示：
得到菱形的分割线做法：连结矩形ABCD的对角线AC、BD（把原矩形分割为四个全等的等腰三角形）；
得到矩形的分割线做法：连结矩形ABCD的对角线BD，分别过点A、C作AE⊥BD于E，CF⊥BD于F（把原矩形分割为四个直角三角形）；
得到平行四边形的分割线做法：连结矩形ABCD的对角线BD，分别过点A、C作AE∥CF，分别交BD于E、F（把原矩形分割为四个三角形）．
得到菱形的分割线做法：连结矩形ABCD的对角线AC、BD（把原矩形分割为四个全等的等腰三角形）；
得到矩形的分割线做法：连结矩形ABCD的对角线BD，分别过点A、C作AE⊥BD于E，CF⊥BD于F（把原矩形分割为四个直角三角形）；
得到平行四边形的分割线做法：连结矩形ABCD的对角线BD，分别过点A、C作AE∥CF，分别交BD于E、F（把原矩形分割为四个三角形）．
点评：此题主要考查了应用设计与作图，正确利用各图形的性质得出是解题关键．
练习册系列答案
相关题目
下列各组数中不能作为直角三角形三边长的是（ ）
| A、1.5，2，2.5 |
| B、7，24，25 |
| C、6，8，10 |
| D、8，12，15 |
如图，直线l1∥l2∥l3，点A、B、C分别在直线l1、l2、l3上．若∠1=70°，∠2=50°，则∠ABC等于（ ）| A、95° | B、100° |
| C、110° | D、120° |
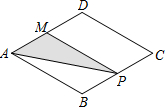如图，菱形ABCD中，AB=2，∠B=120°，点M是AD的中点，点P由点A出发，沿A→B→C→D作匀速运动，到达点D停止，则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是（ ）A、 |
B、 |
C、 |
D、 |
下列调查中，适合采用全面调查方式的是（ ）
| A、对某类烟花爆竹燃放安全情况的调查 |
| B、对端午节期间市场上粽子质量情况的调查 |
| C、了解人们保护水资源的意识 |
| D、学校招聘教师，对应聘人员面试 |
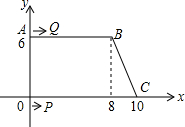如图，在平面直角坐标系中，O（0，0），A（0，6），B（8，6），C（10，0），点Q从点A出发以1cm/s的速度向点B运动，点P从点O出发以2cm/s的速度在线段OC间往返运动，P、Q两点同时出发，当点Q到达点B时，两点同时停止运动．
如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：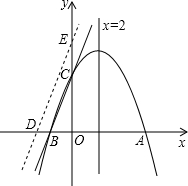
如图，对称轴为直线x=2的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B两点，其中A点的坐标为（5，0）．
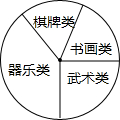某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数：