题目内容
用白铁皮做盒子,每张铁皮可生产12个盒身或者18个盒盖,现有49张铁皮,怎样安排生产盒身和盒盖的铁皮张数,才能使生产的盒身与盒盖配套(一张铁皮只能生产一种产品,一个盒身配两个盒盖)?
考点:二元一次方程组的应用
专题:
分析:根据题意可知,本题中的相等关系是(1)盒身的个数×2=盒盖的个数;(2)制作盒身的铁皮张数+制作盒盖的铁皮张数=49,再列方程组求解.
解答:解:设用x张铁皮制作盒身,y张铁皮制作盒盖,由题意得
,
解得:
.
答:用21张制作盒身,28张制作盒盖,才能使生产的盒身与盒盖配套.
|
解得:
|
答:用21张制作盒身,28张制作盒盖,才能使生产的盒身与盒盖配套.
点评:本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.注意运用本题中隐含的一个相等关系:“一个盒身配两个盒盖”.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
下列说法中,正确的是( )
| A、若两条直角被第三条直线所截,则同旁内角互补 |
| B、相等的角是对顶角 |
| C、三角形的外角等于两个内角的和 |
| D、若三条直线两两相交,则共有6对对顶角 |
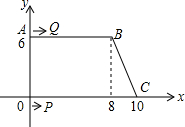 如图,在平面直角坐标系中,O(0,0),A(0,6),B(8,6),C(10,0),点Q从点A出发以1cm/s的速度向点B运动,点P从点O出发以2cm/s的速度在线段OC间往返运动,P、Q两点同时出发,当点Q到达点B时,两点同时停止运动.
如图,在平面直角坐标系中,O(0,0),A(0,6),B(8,6),C(10,0),点Q从点A出发以1cm/s的速度向点B运动,点P从点O出发以2cm/s的速度在线段OC间往返运动,P、Q两点同时出发,当点Q到达点B时,两点同时停止运动.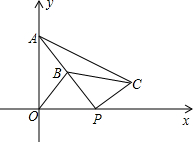 如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.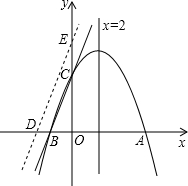 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(5,0).
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(5,0).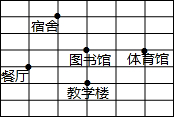 下面是某学校的平面图,请你建立直角坐标系,描述各部门的位置(写出各点的坐标即可).
下面是某学校的平面图,请你建立直角坐标系,描述各部门的位置(写出各点的坐标即可). 如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:
如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题: