题目内容
10. 如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.
如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.(1)写出数轴上点A表示的数为-20.
(2)动点P、Q分别从A、C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=$\frac{1}{3}$CQ.设运动时间为t(t>0)秒.
①写出数轴上点M表示的数为3t-20,点N表示的数为12-t(用含t的式子表示).
②当t=4时,原点O恰为线段MN的中点.
③若动点R从点A出发,以每秒9个单位长度的速度沿数轴向右匀速运动,若P、Q、R三动点同时出发,当点R遇到点Q后,立即返回以原速度向点P运动,当点R遇到点P后,又立即返回以原速度向点Q运动,并不停地以原速度往返于点P与点Q之间,当点P与点Q重合时,点R停止运动.问点R从开始运动到停止运动,行驶的总路程是多少个单位长度?
分析 (1)根据已知条件求得AB的长度,即可写出点A表示的数;
(2)①根据题意画出图形,表示出AP=6t,CQ=3t,再根据线段的中点定义可得AM=3t,根据线段之间的和差关系进而可得到点M表示的数;根据CN=$\frac{1}{3}$CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
②当M在原点O的左侧,根据题意得方程即可得到结论;当M在原点O的右侧,根据题意得方程即可得到结论;
③根据OA=20,OC=12,求得AC=32,于是得到点R从开始运动到停止运动,行驶的总路程=$\frac{32}{6+3}$×9=32个单位长度.
解答 解:(1)∵BC=$\frac{1}{3}$AB=8,
∴AB=24,∵OB比AO的$\frac{1}{4}$少1,
∴AO=20,
∴点A表示的数为:-20.
故答案为:-20,;
(2)①由题意得:AP=6t,CQ=3t,如图1所示:
∵M为AP中点,
∴AM=$\frac{1}{2}$AP=3t,
∴在数轴上点M表示的数是-20+3t,
∵点N在CQ上,CN=$\frac{1}{3}$CQ,
∴CN=t,
∴在数轴上点N表示的数是12-t.
故答案为:3t-20,12-t;
②当M在原点O的左侧,
∵原点O恰为线段MN的中点,
∴OM=ON,
即20-3t=12-t,解得:t=4,
当M在原点O的右侧,
∵原点O恰为线段MN的中点,
∴OM=ON,
即3t-20=t-12,解得:t=4,不合题意舍去,
综上所述:当t=4秒时,O恰为线段MN的中点.
故答案为:4;
③∵OA=20,OC=12,
∴AC=32,
∴点R从开始运动到停止运动,行驶的总路程=$\frac{32}{6+3}$×9=32个单位长度.
答:点R从开始运动到停止运动,行驶的总路程是32个单位长度.
点评 此题主要考查了数轴,以及线段的计算,解决问题的关键是根据题意正确画出图形,要考虑全面各种情况,不要漏解.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 如图,二次函数y=-$\frac{5}{8}$x2+$\frac{7}{4}$x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD,设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )
如图,二次函数y=-$\frac{5}{8}$x2+$\frac{7}{4}$x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD,设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
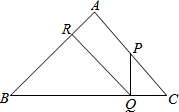 如图,已知:在△ABC中,∠A=90°,AB=AC=1,P是AC上不与A、C重合的一动点,PQ⊥BC于Q,QR⊥AB于R.
如图,已知:在△ABC中,∠A=90°,AB=AC=1,P是AC上不与A、C重合的一动点,PQ⊥BC于Q,QR⊥AB于R. 如图,坐标平面上,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC=10,A点的坐标为(-6,2),B、C两点在方程式y=-6的图形上,D、E两点在y轴上,则F点的纵坐标为2,则直线EF解析式为y=$\frac{3}{4}$x-4.
如图,坐标平面上,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC=10,A点的坐标为(-6,2),B、C两点在方程式y=-6的图形上,D、E两点在y轴上,则F点的纵坐标为2,则直线EF解析式为y=$\frac{3}{4}$x-4.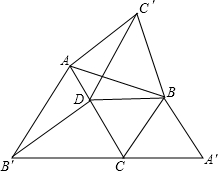 如图,△ABC中,∠ACB=60°,△ABC′,△BCA′,△CAB′都是△ABC形外的等边三角形,点D在边AC 上,且DC=BC.连接DB,DB′,DC′.有下列结论:
如图,△ABC中,∠ACB=60°,△ABC′,△BCA′,△CAB′都是△ABC形外的等边三角形,点D在边AC 上,且DC=BC.连接DB,DB′,DC′.有下列结论: 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为ts(0<t<6),试尝试探究下列问题:
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为ts(0<t<6),试尝试探究下列问题: