题目内容
5.甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.从袋中随机摸出一球后放回,摇匀后再随机摸出一球.现制定如下游戏规则:若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏规则对双方是否公平?请说明理由.若不公平,你认为应该修改游戏规则才能使得规则对双方公平?分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果,即可求得求概率,比较大小,即可知这个游戏是否公平.
解答 解:画树状图得: ,
,
由图可得共有9种等可能的结果为:2,3,4,3,4,5,4,5,6;
∵两次摸出的球的标号之和为偶数的有5种情况,两次摸出的球的标号之和为奇数的有4种情况,
∴P(甲胜)=$\frac{5}{9}$,P(乙胜)=$\frac{4}{9}$.
∴P(甲胜)≠P(乙胜),
故这个游戏不公平,
可改规则为两次摸出的球的标号之和大于4甲胜,两次摸出的球的标号之和小于4乙胜.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
相关题目
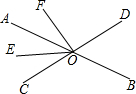 如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°.求∠AOF的度数.
如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°.求∠AOF的度数.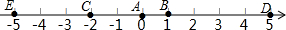 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499. 如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.
如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.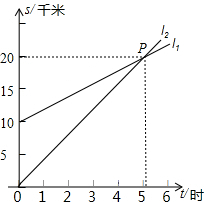 如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:
如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:


