题目内容
2. 如图,坐标平面上,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC=10,A点的坐标为(-6,2),B、C两点在方程式y=-6的图形上,D、E两点在y轴上,则F点的纵坐标为2,则直线EF解析式为y=$\frac{3}{4}$x-4.
如图,坐标平面上,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC=10,A点的坐标为(-6,2),B、C两点在方程式y=-6的图形上,D、E两点在y轴上,则F点的纵坐标为2,则直线EF解析式为y=$\frac{3}{4}$x-4.
分析 如图,作辅助线;证明△AKC≌△CHA,即可求得CK=AH=8,证明∠BAC=∠EDF,AC=DF,进而证明△AKC≌△DPF,即可求得E、F点的坐标,然后根据待定系数法即可求得解析式.
解答 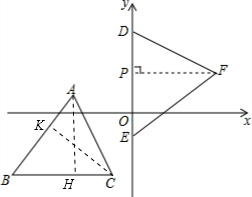 解:如图,在△ABC中,分别作高线AH、CK,则∠AKC=∠CHA.
解:如图,在△ABC中,分别作高线AH、CK,则∠AKC=∠CHA.
∵AB=BC,
∴∠BAC=∠BCA.
在△AKC和△CHA中,
$\left\{\begin{array}{l}{∠AKC=∠CHA}\\{∠BAC=∠BCA}\\{AC=CA}\end{array}\right.$,
∴△AKC≌△CHA(AAS),
∴CK=AH.
∵A点的坐标为(-6,2),
B、C两点的纵坐标均为-6,
∴AH=8.
又∵CK=AH,
∴CK=AH=8.
∵AB=BC=10,
∴BK=$\sqrt{B{C}^{2}-C{K}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴AK=10-6=4,
∵△ABC≌△DEF,
∴∠BAC=∠EDF,AC=DF,DE=AB=10.
在△AKC和△DPF中,
$\left\{\begin{array}{l}{∠AKC=∠DPF}\\{∠BAC=∠EDF}\\{AC=DF}\end{array}\right.$,
∴△AKC≌△DPF(AAS),
∴PF=KC=8,DP=AK=4.
∴PE=10-4=6,
∵F点的纵坐标为2,
∴E(0,-4),F(8,2),
设直线EF的解析式为y=kx-4,
代入F(8,2)得,2=8k-4,
解得k=$\frac{3}{4}$,
∴直线EF解析式为y=$\frac{3}{4}$x-4.
故答案为y=$\frac{3}{4}$x-4.
点评 该题主要考查了全等三角形的判定及其性质以及待定系数法求一次函数的解析式;解题的关键是作辅助线,构造全等三角形,灵活运用全等三角形的判定及其性质来分析、判断、推理或解答.

 能考试期末冲刺卷系列答案
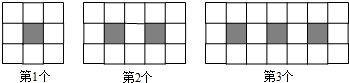
能考试期末冲刺卷系列答案| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x | x x x y y x x y y x x x | x x x x y y y x x y y y x x y y y x x x x | … |
(1)第2格的“特征多项式”为9x+4y,第n格的“特征多项式”为(n+1)2x+n2y;(n为正整数)
(2)若第1格的“特征多项式”的值为-8,第2格的“特征多项式”的值为-11.
①求x,y的值;
②在此条件下,第n格的特征多项式是否有最小值?若有,求最小值和相应的n值;若没有,请说明理由.
| 数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
| 价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发600千克苹果,则他在A家批发需要3312元,在B家批发需要3360元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A家批发需要5.4x元,在B家批发需要4.5x-1200元(用含x的代数式表示);
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
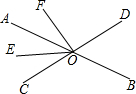 如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°.求∠AOF的度数.
如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°.求∠AOF的度数. 如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.
如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.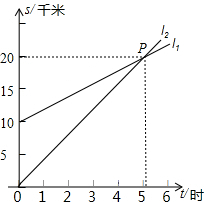 如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:
如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空: