题目内容
 如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.
如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.(1)请说出旋转中心及旋转角度;
(2)若连接PQ,试判断△PBQ的形状;
(3)若∠BPA=135°,试说明点A,P,Q三点在同一直线上;
(4)若∠BPA=135°,AP=3,PB=
| 2 |
(5)在(4)的条件下,求线段AP在旋转过程中所扫过的面积.
考点:旋转的性质,正方形的性质,扇形面积的计算
专题:计算题
分析:(1)先利用正方形的性质得BA=BC,∠ABC=90°,然后根据旋转的性质确定旋转中心和旋转角度;
(2)根据旋转的性质得BQ=BP,∠QBP=90°,可判断△PBQ为等腰直角三角形;
(3)根据等腰直角三角形的性质得∠BPQ=∠BQP=45°,而∠BPA=135°,则∠BPA+∠BPQ=180°,由此可判断点A,P,Q三点在同一直线上;
(4)根据旋转的性质得∠BQC=∠BPQ=135°,CQ=AP=3,而∠BQP=45°,所以∠AQC=∠BQC-∠BQP=90°,再利用△PBQ为等腰直角三角形得到PQ=
BP=2,则AQ=AP+PQ=5,在Rt△AQC中,根据勾股定理可计算出AC=
;
(5)由AC=
,根据正方形的性质得AB=
,然后利用线段AP在旋转过程中所扫过的面积=S扇形BAC-S扇形BPQ和扇形的面积公式进行计算.
(2)根据旋转的性质得BQ=BP,∠QBP=90°,可判断△PBQ为等腰直角三角形;
(3)根据等腰直角三角形的性质得∠BPQ=∠BQP=45°,而∠BPA=135°,则∠BPA+∠BPQ=180°,由此可判断点A,P,Q三点在同一直线上;
(4)根据旋转的性质得∠BQC=∠BPQ=135°,CQ=AP=3,而∠BQP=45°,所以∠AQC=∠BQC-∠BQP=90°,再利用△PBQ为等腰直角三角形得到PQ=
| 2 |
| 34 |
(5)由AC=
| 34 |
| 17 |
解答:解:(1)∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∴△ABP旋转后到达△CBQ的位置,其旋转中心为点B,旋转角为90°;
(2)如图,
∵△ABP绕B点顺时针旋转90°到达△CBQ的位置,
∴BQ=BP,∠QBP=90°,
∴△PBQ为等腰直角三角形;
(3)∵△PBQ为等腰直角三角形,
∴∠BPQ=∠BQP=45°,
而∠BPA=135°,
∴∠BPA+∠BPQ=135°+45°=180°,
∴点A,P,Q三点在同一直线上;
(4)∵△ABP绕B点顺时针旋转90°到达△CBQ的位置,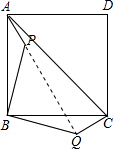
∴∠BQC=∠BPQ=135°,CQ=AP=3,
而∠BQP=45°,
∴∠AQC=∠BQC-∠BQP=90°,
∵△PBQ为等腰直角三角形,
∴PQ=
BP=
×
=2,
∴AQ=AP+PQ=3+2=5,
在Rt△AQC中,AC=
=
;
(5)∵AC=
,
∴AB=
=
,
线段AP在旋转过程中所扫过的面积=S扇形BAC-S扇形BPQ=
-
=
π.
∴BA=BC,∠ABC=90°,
∴△ABP旋转后到达△CBQ的位置,其旋转中心为点B,旋转角为90°;
(2)如图,
∵△ABP绕B点顺时针旋转90°到达△CBQ的位置,
∴BQ=BP,∠QBP=90°,
∴△PBQ为等腰直角三角形;
(3)∵△PBQ为等腰直角三角形,
∴∠BPQ=∠BQP=45°,
而∠BPA=135°,
∴∠BPA+∠BPQ=135°+45°=180°,
∴点A,P,Q三点在同一直线上;
(4)∵△ABP绕B点顺时针旋转90°到达△CBQ的位置,

∴∠BQC=∠BPQ=135°,CQ=AP=3,
而∠BQP=45°,
∴∠AQC=∠BQC-∠BQP=90°,
∵△PBQ为等腰直角三角形,
∴PQ=
| 2 |
| 2 |
| 2 |
∴AQ=AP+PQ=3+2=5,
在Rt△AQC中,AC=
| AQ2+CQ2 |
| 34 |
(5)∵AC=
| 34 |
∴AB=
| AC | ||
|
| 17 |
线段AP在旋转过程中所扫过的面积=S扇形BAC-S扇形BPQ=
90•π•(
| ||
| 360 |
90•π•(
| ||
| 360 |
| 15 |
| 4 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质、等腰直角三角形的性质以及扇形的面积公式.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
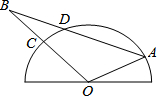 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B的度数为( )
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B的度数为( )| A、20° | B、30° |
| C、45° | D、60° |
已知△ABC中,∠A=2∠B=3∠C,则△ABC为( )
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
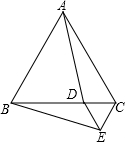 如图,△ABC和△DCE都是等边三角形,点D是△ABC的边BC上的一点,连接AD,BE.求证:AD=BE.
如图,△ABC和△DCE都是等边三角形,点D是△ABC的边BC上的一点,连接AD,BE.求证:AD=BE. 如图,在7×8的方格纸中,已知图中每个小正方形的边长都为1,求图中阴影部分的面积.
如图,在7×8的方格纸中,已知图中每个小正方形的边长都为1,求图中阴影部分的面积. 如图,在矩形ABCD中,M是BC的中点,MA⊥MD.若矩形的周长为48cm,求矩形的面积.
如图,在矩形ABCD中,M是BC的中点,MA⊥MD.若矩形的周长为48cm,求矩形的面积. 如图,等腰梯形ABCD是一个四棱柱的俯视图,它的高为5,AD=3,AE⊥BC于点E,AE=4,BC=7,求此四棱柱的三种视图的面积和.
如图,等腰梯形ABCD是一个四棱柱的俯视图,它的高为5,AD=3,AE⊥BC于点E,AE=4,BC=7,求此四棱柱的三种视图的面积和.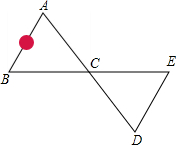 如固,为修筑一条公路,需测量出被大石头阻挡的∠BAC的大小,为此,小张师傅便在直线AC上取点D,使AC=CD,在BC的延长线上取点E,使BC=CE,连接DE,只要测出∠D的度数,则可知∠A的度数等于∠D的度数.请说明理由.
如固,为修筑一条公路,需测量出被大石头阻挡的∠BAC的大小,为此,小张师傅便在直线AC上取点D,使AC=CD,在BC的延长线上取点E,使BC=CE,连接DE,只要测出∠D的度数,则可知∠A的度数等于∠D的度数.请说明理由. 已知线段a,h(如图1、2),求作△ABC,使AB=AC=a,高AD=h.
已知线段a,h(如图1、2),求作△ABC,使AB=AC=a,高AD=h.