题目内容
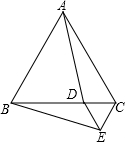 如图,△ABC和△DCE都是等边三角形,点D是△ABC的边BC上的一点,连接AD,BE.求证:AD=BE.
如图,△ABC和△DCE都是等边三角形,点D是△ABC的边BC上的一点,连接AD,BE.求证:AD=BE.考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:根据全等三角形的判定定理SAS证得△BCE≌△ACD,然后由全等三角形的对应边相等知AD=BE.
解答:证明:∵△ABC、△ECD都是等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=60°,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE(全等三角形的对应边相等).
∴AC=BC,EC=DC,∠ACB=∠ECD=60°,
在△BCE和△ACD中,
|
∴△BCE≌△ACD(SAS),
∴AD=BE(全等三角形的对应边相等).
点评:本题综合考查了等边三角形的性质、全等三角形的判定与性质.等边三角形的三条边都相等,三个内角都是60°.

练习册系列答案
相关题目
对于抛物线y=-x2+2x-3,下列结论正确的是( )
| A、与x轴有两个交点 |
| B、开口向上 |
| C、与y轴交点坐标是(0,-3) |
| D、顶点坐标是(1,2) |
△ABC的三个内角∠A、∠B、∠C满足∠A:∠B:∠C=1:2:3,则这个三角形是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、任意三角形 |
 如图,在△ABC中,BD=2DC,CE=2EA,AD与BE交于点F,且△ABC的面积为42,则△AEF的面积是多少?
如图,在△ABC中,BD=2DC,CE=2EA,AD与BE交于点F,且△ABC的面积为42,则△AEF的面积是多少? 如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.
如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置. 如图,AB=AC,∠B=∠C,求证:△ABD≌△ACE.
如图,AB=AC,∠B=∠C,求证:△ABD≌△ACE.