题目内容
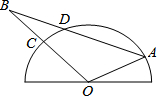如图，半圆O是一个量角器，△AOB为一纸片，AB交半圆于点D，OB交半圆于点C，若点C、D、A在量角器上对应读数分别为45°，70°，160°，则∠B的度数为（ ）| A、20° | B、30° |
| C、45° | D、60° |
考点：圆的认识,三角形的外角性质
专题：计算题
分析：连结OD，如图，根据题意得∠DOC=25°，∠AOD=90°，由于OD=OA，则∠ADO=45°，然后利用三角形外角性质得∠ADO=∠B+∠DOB，所以∠B=45°-25°=20°．
解答：
解：连结OD，如图，则∠DOC=70°-45°=25°，∠AOD=160°-70°=90°，
∵OD=OA，
∴∠ADO=45°，
∵∠ADO=∠B+∠DOB，
∴∠B=45°-25°=20°．
故选A．
解：连结OD，如图，则∠DOC=70°-45°=25°，∠AOD=160°-70°=90°，∵OD=OA，
∴∠ADO=45°，
∵∠ADO=∠B+∠DOB，
∴∠B=45°-25°=20°．
故选A．
点评：本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．
练习册系列答案
相关题目
下列计算正确的个数是（ ）
①a5•a5=a10；②b5+b5=b10；③x5•x5=x25；④y5•y5=2y10；⑤c•c3=c3；⑥m•m3=m4；⑦（-x）•（-x）2=-x3；⑧y•y2•y4=y7．
①a5•a5=a10；②b5+b5=b10；③x5•x5=x25；④y5•y5=2y10；⑤c•c3=c3；⑥m•m3=m4；⑦（-x）•（-x）2=-x3；⑧y•y2•y4=y7．
| A、2 | B、3 | C、4 | D、5 |
下列命题不正确的是（ ）
| A、角平分钱上的点到角两边的距离相等 |
| B、两边对应成比等且有一个角对应相等的两个三角形相似 |
| C、位似的两个图形一定相似 |
| D、三角函数值的大小与角两边的长短无关 |
对于抛物线y=-x2+2x-3，下列结论正确的是（ ）
| A、与x轴有两个交点 |
| B、开口向上 |
| C、与y轴交点坐标是（0，-3） |
| D、顶点坐标是（1，2） |
如果把分式
中的x和y都扩大2倍，那么分式的值（ ）
| x+y |
| 2xy |
| A、不变 | B、扩大2倍 |
| C、扩大4倍 | D、缩小2倍 |
计算（-2）2010+（-2）2011的值是（ ）
| A、-22010 |
| B、-2 |
| C、22010 |
| D、（-2）2011 |
工人师傅对如图所示的零件进行加工，把材料弯成了一个40°的锐角，然后准备在A处第二次加工拐弯，要保证弯过来的部分与BC保持平行，弯的角度是（ ）| A、40° | B、140° |
| C、40°或140° | D、50° |
△ABC的三个内角∠A、∠B、∠C满足∠A：∠B：∠C=1：2：3，则这个三角形是（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、任意三角形 |
如图，已知P为正方形ABCD内一点，△ABP经过旋转后到达△CBQ的位置．