题目内容
 如图,在矩形ABCD中,M是BC的中点,MA⊥MD.若矩形的周长为48cm,求矩形的面积.
如图,在矩形ABCD中,M是BC的中点,MA⊥MD.若矩形的周长为48cm,求矩形的面积.考点:矩形的性质
专题:
分析:根据矩形的性质求出∠CDM=∠BMA,∠DMC=∠BAM继而求出△DCM∽△MBA.然后求出AB=BM,(AB+2AB)×2=48可求出AB,BC的值.最后可求出矩形ABCD的面积.
解答:解:∠CDM+∠CMD=90°,∠CMD+∠BMA=90°,
∴∠CDM=∠BMA,同理∠DMC=∠BAM.
∴△DCM∽△MBA.
∴
=
,
∵DC=AB,BM=CM,
∴AB=BM.
又∵(AB+BC)×2=48,
∴(AB+2AB)×2=48.
∴AB=8,BC=16.
∴矩形ABCD的面积为128.
∴∠CDM=∠BMA,同理∠DMC=∠BAM.
∴△DCM∽△MBA.
∴
| DC |
| MB |
| CM |
| AB |
∵DC=AB,BM=CM,
∴AB=BM.
又∵(AB+BC)×2=48,
∴(AB+2AB)×2=48.
∴AB=8,BC=16.
∴矩形ABCD的面积为128.
点评:本题的关键是利用了三角形相似的判定定理,及相似三角形的性质和矩形的性质.

练习册系列答案
相关题目
计算(-2)2010+(-2)2011的值是( )
| A、-22010 |
| B、-2 |
| C、22010 |
| D、(-2)2011 |
 如图,在△ABC中,BD=2DC,CE=2EA,AD与BE交于点F,且△ABC的面积为42,则△AEF的面积是多少?
如图,在△ABC中,BD=2DC,CE=2EA,AD与BE交于点F,且△ABC的面积为42,则△AEF的面积是多少? 如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.
如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置. 如图,AB=AC,∠B=∠C,求证:△ABD≌△ACE.
如图,AB=AC,∠B=∠C,求证:△ABD≌△ACE.
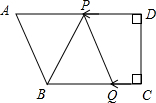 如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q三点为顶点的三角形为等腰三角形?
如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q三点为顶点的三角形为等腰三角形?