题目内容
14.已知:△ABC,AB=1,∠B=60°,∠C=15°,D为直线AB上一点,且BD=BC,则△ACD的面积等于$\frac{9\sqrt{3}}{4}$+$\frac{15}{4}$.分析 如图在BC上取一点E使得AE=EC,作AF⊥CD垂足为F,在RT△ABE可以求出线段BE、AE,再在RT△ADF中求出AF,BF,在RT△AFC中求出CF,根据S△ACD=$\frac{1}{2}$•CD•AF即可计算.
解答 解:如图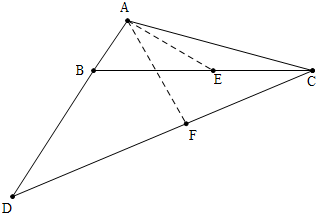 ,在BC上取一点E使得AE=EC,作AF⊥CD垂足为F.
,在BC上取一点E使得AE=EC,作AF⊥CD垂足为F.
∵∠ACB=15°,
∴∠EAC=∠ACE=15°,
∴∠AEB=∠EAC+∠ACE=30°,
在RT△ABE中,∵AB=1,∠AEB=30°,
∴BE=2,AE=EC=$\sqrt{3}$,
∴BD=BC=2+$\sqrt{3}$,AD=3+$\sqrt{3}$,
∴∠BDC=∠DCB
∵∠ABC=60°,∠ABC=∠BDC+∠DCB,
∴∠D=∠BCD=30°,∠ACF=45°
在RT△ADF中,∵∠D=30°,AD=3+$\sqrt{3}$,
∴AF=$\frac{1}{2}$AB=$\frac{3}{2}$+$\frac{\sqrt{3}}{2}$,DF=$\frac{3\sqrt{3}}{2}+\frac{3}{2}$,
∵∠AFC=90°,
∴∠FAC=∠ACF=45°,
∴$AF=FC=\frac{3}{2}+\frac{\sqrt{3}}{2}$,
∴CD=DF+CF=2$\sqrt{3}$+3,
∴S△ACD=$\frac{1}{2}$•CD•AF=$\frac{1}{2}$×(2$\sqrt{3}$+3)($\frac{3}{2}$+$\frac{\sqrt{3}}{2}$)=$\frac{9\sqrt{3}}{4}$+$\frac{15}{4}$.
故答案为$\frac{9\sqrt{3}}{4}$+$\frac{15}{4}$.
点评 本题考查直角三角形的有关性质,解题的关键是利用特殊角30度角的性质,体现了转化的思想“15°”如何转化为“30°”这是添加辅助线的依据.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案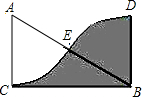 如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )
如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
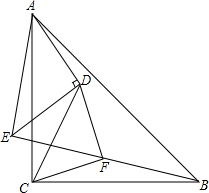 如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.
如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°. 如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE,连接AE,若AB=2cm,CD=3cm,过B点作BF⊥AB,过点E作EG⊥AB交AB的延长线于点G,试求△ABE的面积.
如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE,连接AE,若AB=2cm,CD=3cm,过B点作BF⊥AB,过点E作EG⊥AB交AB的延长线于点G,试求△ABE的面积.