题目内容
4.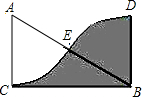 如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )
如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
分析 “扇形ACE与扇形BDE关于点E中心对称”则阴影部分的面积等于S△ABC,根据已知条件求出S△ABC即可.
解答 解:∵扇形ACE与扇形BDE关于点E中心对称,
∴AE=BE=AC,
∴AB=$\frac{1}{2}$AC,
∴∠A=60°,
∴AC=$\frac{\sqrt{3}}{3}$BC=2,
∴图中阴影部分的面积=S△ABC=$\frac{1}{2}$•AC•BC
=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$.
故选B.
点评 本题考查了扇形的面积的计算,解题的关键是能够利用条件知道“扇形ACE与扇形BDE关于点E中心对称”则阴影部分的面积等于S△ABC,运用勾股定理求出相关的数据求解.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
13.己知方程2xa+b-xa-b-ab=0是关于x的一元二次方程,则对应a、b的值有( )
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |

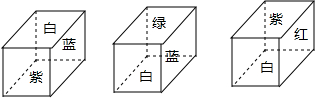 一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色,其中红、白、黄、绿、蓝、紫,分别代表的是数字-1、-2、-3、-4、-5、-6中的一个数,如图是这个正方体的三种放置方法,若三个正方体下底面所标颜色代表的数字分别是a,b,c,则a+b+c+abc=-85.
一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色,其中红、白、黄、绿、蓝、紫,分别代表的是数字-1、-2、-3、-4、-5、-6中的一个数,如图是这个正方体的三种放置方法,若三个正方体下底面所标颜色代表的数字分别是a,b,c,则a+b+c+abc=-85.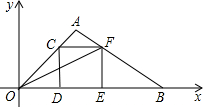 在直角坐标系中,O为坐标原点,点A的坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,若以B,E,F为顶点的三角形与△OFE相似,B点的坐标是($\frac{3}{2}$,0)(3,0).
在直角坐标系中,O为坐标原点,点A的坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,若以B,E,F为顶点的三角形与△OFE相似,B点的坐标是($\frac{3}{2}$,0)(3,0).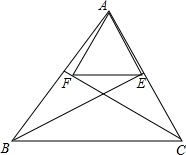 如图,过△ABC的顶点A向∠ABC和∠ACB的平分线作垂线,其垂足分别为E,F,求证:EF∥BC.
如图,过△ABC的顶点A向∠ABC和∠ACB的平分线作垂线,其垂足分别为E,F,求证:EF∥BC.