题目内容
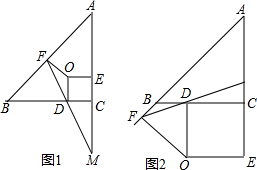
9. 如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE,连接AE,若AB=2cm,CD=3cm,过B点作BF⊥AB,过点E作EG⊥AB交AB的延长线于点G,试求△ABE的面积.
如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE,连接AE,若AB=2cm,CD=3cm,过B点作BF⊥AB,过点E作EG⊥AB交AB的延长线于点G,试求△ABE的面积.
分析 求出四边形ABFD是矩形,根据矩形的对边相等可得AB=DF=2,然后求出CF=1,再求出∠FBC=∠EBG,然后利用“角角边”证明△FBC和△GBE全等,根据全等三角形对应边相等可得EG=CF=1,再利用三角形的面积公式列式计算即可得解.
解答 解:如图:
∵AB⊥AD,CD⊥AD,BF⊥DC,
∴∠D=∠BAD=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD,AB=DF=2,∠BFC=∠FBG=90°,
∵DC=3,DF=2,
∴CF=DC-DF=3-2=1,
∵BC以点B为旋转中心,逆时针方向旋转90°至点E,
∴∠CBE=90°,BC=BE,
∵∠ebc=∠fbg=90°,
∴∠CBF=∠EBG=90°-∠CBG,
∴∠CDF=∠EDG,
在△BFC和△BGE中,
$\left\{\begin{array}{l}{∠BFC=∠G}\\{∠FBC=∠EBG}\\{BC=BE}\end{array}\right.$,
∴△BFC≌△BGE(AAS),
∴EG=CF=1,
∴△ABE的面积=$\frac{1}{2}$AB•EG=$\frac{1}{2}$×2×1=1.
点评 本题考查了直角梯形,全等三角形的判定与性质,旋转变换的性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△ABD与△ACE都是等腰直角三角形,∠BAD=∠CAE=90°.
如图,△ABD与△ACE都是等腰直角三角形,∠BAD=∠CAE=90°.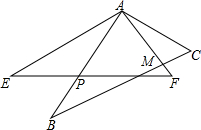 如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠BAE=24°,∠F=57°,边BC与AF相交于点M,边AB与EF相交于点P.
如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠BAE=24°,∠F=57°,边BC与AF相交于点M,边AB与EF相交于点P.