题目内容
如果不等式组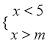 有解,那么m的取值范围是( )
有解,那么m的取值范围是( )
A. m>5 B. m≥5 C. m<5 D. m≤8
 C
【解析】∵不等式组有解,
∴m<5.
故选:C.
C
【解析】∵不等式组有解,
∴m<5.
故选:C.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算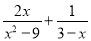 的结果是( )
的结果是( )
A. 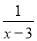 B.
B. 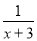 C.
C. 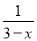 D.
D. 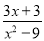
 B
【解析】原式=?===.
故选:B.
B
【解析】原式=?===.
故选:B. “二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
 【解析】
(1)设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆,
根据题意得: ,解得: 。
答:“益安”车队载重量为8吨的卡车有5辆,10吨的卡车有7辆。
(2)设载重量为8吨的卡车增加了z辆,
依题意得:8(5+z)+10(7+6﹣z)>165,解得:z<。
∵z≥0且为整数,∴z=0,1,2,6﹣z=6,5,4。
∴车队共有3种购车方案:
...
【解析】
(1)设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆,
根据题意得: ,解得: 。
答:“益安”车队载重量为8吨的卡车有5辆,10吨的卡车有7辆。
(2)设载重量为8吨的卡车增加了z辆,
依题意得:8(5+z)+10(7+6﹣z)>165,解得:z<。
∵z≥0且为整数,∴z=0,1,2,6﹣z=6,5,4。
∴车队共有3种购车方案:
... 解不等式,并把解集在数轴上表示出来:
(1)5x﹣6≤2(x+3);
(2)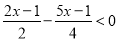
 (1)x≤4; (2)x>﹣1,
【解析】【试题分析】(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
【试题解析】(1)去括号,得:5x﹣6≤2x+6,
移项,得:5x﹣2x≤6+6,
合并同类项,得:3x≤12,
系数化为1,得:x≤4,
...
(1)x≤4; (2)x>﹣1,
【解析】【试题分析】(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
【试题解析】(1)去括号,得:5x﹣6≤2x+6,
移项,得:5x﹣2x≤6+6,
合并同类项,得:3x≤12,
系数化为1,得:x≤4,
... 若a>c,则当m_________时,am<cm; 当m_________时,am=cm.
 <0 =0
【解析】根据不等式的基本性质:不等式两边乘(或除以)同一个负数,不等号的方向改变,可知m<0.
∵a>c,
又知:am<cm,
∴根据不等式的基本性质3可得:
m<0;
又知:am=cm,
∴m=0.
故答案为:<0;=0.
<0 =0
【解析】根据不等式的基本性质:不等式两边乘(或除以)同一个负数,不等号的方向改变,可知m<0.
∵a>c,
又知:am<cm,
∴根据不等式的基本性质3可得:
m<0;
又知:am=cm,
∴m=0.
故答案为:<0;=0. 如图,当y<0时,自变量x的范围是( )
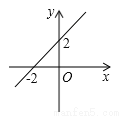
A.x<-2 B.x>-2 C.x<2 D.x>2
 A.
【解析】
试题解析:由图象可得,一次函数的图象与x轴的交点为(-2,0),当y<0时,x<-2.
故选A.
A.
【解析】
试题解析:由图象可得,一次函数的图象与x轴的交点为(-2,0),当y<0时,x<-2.
故选A. 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2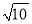 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
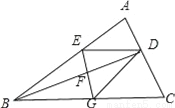
 (1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:...
(1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:... 如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
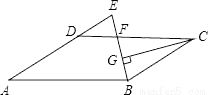
A. 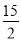 B.
B. 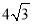 C.
C. 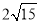 D.
D. 
 C
【解析】∵∠ABC的平分线交CD于点F,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,
∴DE=4,
∵DC∥AB,
∴,
∴,
∴EB=6,
∵CF=CB,CG⊥BF,
∴BG=BF=2...
C
【解析】∵∠ABC的平分线交CD于点F,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,
∴DE=4,
∵DC∥AB,
∴,
∴,
∴EB=6,
∵CF=CB,CG⊥BF,
∴BG=BF=2... (2016辽宁省沈阳市)如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.
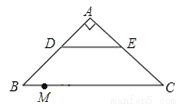
 或.
【解析】由图可知,在△OMN中,∠OMN的度数是一个定值,且∠OMN不为直角. 故当∠ONM=90°或∠MON=90°时,△OMN是直角三角形. 因此,本题需要按以下两种情况分别求解.
(1) 当∠ONM=90°时,则DN⊥BC.
过点E作EF⊥BC,垂足为F.(如图)
∵在Rt△ABC中,∠A=90°,AB=AC,
∴∠C=45°,
∵BC=20,
...
或.
【解析】由图可知,在△OMN中,∠OMN的度数是一个定值,且∠OMN不为直角. 故当∠ONM=90°或∠MON=90°时,△OMN是直角三角形. 因此,本题需要按以下两种情况分别求解.
(1) 当∠ONM=90°时,则DN⊥BC.
过点E作EF⊥BC,垂足为F.(如图)
∵在Rt△ABC中,∠A=90°,AB=AC,
∴∠C=45°,
∵BC=20,
... 
