题目内容
如图，当y＜0时，自变量x的范围是（ ）
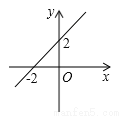
A．x＜-2 B．x＞-2 C．x＜2 D．x＞2
A．
【解析】
试题解析：由图象可得，一次函数的图象与x轴的交点为（-2，0），当y＜0时，x＜-2．
故选A．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案某工厂用如图甲所示的长方形和正方形纸板，做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒．
（1）现有正方形纸板162张，长方形纸板340张．若要做两种纸盒共100个，设做竖式纸盒x个．
①根据题意，完成以下表格：
纸盒 纸板 | 竖式纸盒（个） | 横式纸盒（个） |
x | 100﹣x | |
正方形纸板（张） | 2（100﹣x） | |
长方形纸板（张） | 4x |
②按两种纸盒的生产个数来分，有哪几种生产方案？
（2）若有正方形纸162张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完．已知290＜a＜306．求a的值．
（1）①见解析；②有三种方案：生产竖式纸盒38个，横式纸盒62个；生产竖式纸盒39个，横式纸盒61个；生产竖式纸盒40个，横式纸盒60个；
（2）293或298或303（写出其中一个即可）．
【解析】试题分析：（1）①可根据竖式纸盒+横式纸盒=100个，每个竖式纸盒需1个正方形纸板和4个长方形纸板，每个横式纸盒需3个长方形纸板和2个正方形纸板来填空．
②生产竖式纸盒用的正方形纸板... 某商人从批发市场买了20千克肉，每千克a元，又从肉店买了10千克肉，每千克b元，最后他又以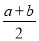
元的单价把肉全部卖掉，结果赔了钱，原因是（ ）
A. a＞b B. a＜b C. a=b D. 与a和b的大小无关
A
【解析】【解析】
根据题意得：（20a+10b）÷30﹣= = =，
当a＞b，即a﹣b＞0时，结果赔钱．故选A． 不等式组﹣1＜x﹣5＜11的解集是_________．
4＜x＜16
【解析】不等式每个部分都加5得，4＜x＜16．
故答案为：4＜x＜16． 如果不等式组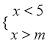
有解，那么m的取值范围是（ ）
A. m＞5 B. m≥5 C. m＜5 D. m≤8
C
【解析】∵不等式组有解，
∴m＜5．
故选：C． 我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
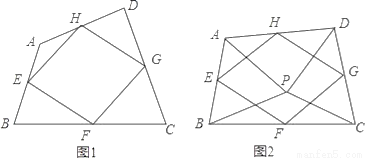
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）
（1）证明见解析；（2）四边形EFGH是菱形，证明见解析；（3）四边形EFGH是正方形.
【解析】试题分析：（1）如图1中，连接BD，根据三角形中位线定理只要证明EH∥FG，EH=FG即可．
（2）四边形EFGH是菱形．先证明△APC≌△BPD，得到AC=BD，再证明EF=FG即可．
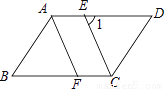
（3）四边形EFGH是正方形，只要证明∠EHG=90°，利用△APC≌△BPD，得∠ACP=∠B... 已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．
（1）求证：△ABF≌△CDE；
（2）如图，若∠1=65°，求∠B的大小．
（1）证明见解析；（2）50°．
【解析】试题分析：（1）由平行四边形的性质得出AB=CD，AD∥BC，∠B=∠D，得出∠1=∠DCE，证出∠AFB=∠1，由AAS证明△ABF≌△CDE即可；（2）由（1）得∠1=∠DCE=65°，由平行四边形的性质和三角形内角和定理即可得出结果．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AB=CD，AD∥BC，∠B=∠D， ∴∠1=∠DCE... 如图，在△ABC中，AB=4，BC=6，DE、DF是△ABC的中位线，则四边形BEDF的周长是（ ）
A．5 B．7 C．8 D．10
D．
【解析】
试题分析：∵AB=4，BC=6，DE、DF是△ABC的中位线，∴DE=AB=2，DF=BC=3，DE∥BF，DF∥BE，∴四边形BEDF为平行四边形，∴四边形BEDF的周长为：2×2+3×2=10，故选D． 一个多边形的内角和是外角和的2倍，则这个多边形的边数为______．
6
【解析】∵多边形的外角和是360度，多边形的内角和是外角和的2倍，
则内角和是720度，
720÷180+2=6，
∴这个多边形是六边形，
故答案为：6．