题目内容
3.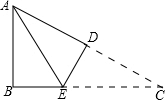 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )| A. | 4cm | B. | $\frac{3}{2}$cm | C. | $\frac{25}{8}$cm | D. | $\frac{7}{2}$cm |
分析 设AE=xcm,根据勾股定理求出BC,用x表示出BE,根据勾股定理列出方程,解方程即可.
解答 解:设AE=xcm,由翻折变换的性质可知,EC=xcm,
∵∠B=90°,AB=3cm,AC=5cm,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=4cm,
∴BE=BC-CE=(4-x)cm,
在Rt△ABE中,AE2=AB2+BE2,即x2=32+(4-x)2,
解得,x=$\frac{25}{8}$,
故选:C.
点评 本题考查的是翻折变换的性质和勾股定理的应用,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
14.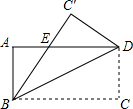 如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )
如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )
 如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )
如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 2$\sqrt{3}$ |
8.通过统计甲、乙、丙、丁四名同学某学期的四次数学测试成绩,得到甲、乙、丙、丁三明同学四次数学测试成绩的方差分别为S甲2=17,S乙2=36,S丙2=14,丁同学四次数学测试成绩(单位:分)
如下表:
则这四名同学四次数学测试成绩最稳定的是( )
如下表:
| 第一次 | 第二次 | 第三次 | 第四次 | |
| 丁同学 | 80 | 80 | 90 | 90 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
15.和睦社区一次歌唱比赛共500名选手参加,比赛分数均大于或等于60且小于100,分数段的频率分布情况如表所示(其中每个分数段可包括最小值,不包括最大值),结合表中的信息,可得比赛分数在80~90分数段的选手有150名.
| 分数段 | 60~70 | 70~80 | 80~90 | 90~100 |
| 频率 | 0.2 | 0.25 | 0.25 |
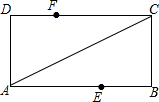 如图,矩形ABCD中,AB=2,BC=4,将矩形沿对角线AC翻折,使AB边上的点E与CD边上的点F重合,则AE的长是2.5.
如图,矩形ABCD中,AB=2,BC=4,将矩形沿对角线AC翻折,使AB边上的点E与CD边上的点F重合,则AE的长是2.5.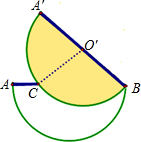 将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形,$\widehat{AB}$与直径AB交于点C,连接点C与圆心O′.
将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形,$\widehat{AB}$与直径AB交于点C,连接点C与圆心O′.