题目内容
13.解不等式$\left\{\begin{array}{l}{5x-4>3x}\\{13-2(3x-2)≤3}\end{array}\right.$,并在数轴上表示不等式组的解.分析 分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,表示在数轴上即可.
解答 解:$\left\{\begin{array}{l}{5x-4>3x①}\\{13-2(3x-2)≤3②}\end{array}\right.$,
由①得:x>2,
由②得:x≥$\frac{7}{3}$,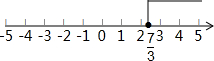
则不等式组的解集为x≥$\frac{7}{3}$.
点评 此题考查了解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
1.在${\frac{1}{x}}、{\frac{1}{3}}、{\frac{{{x^2}+1}}{2}}、{\frac{5+y}{π}}、\frac{{{a^2}+1}}{a^2}$中分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
3.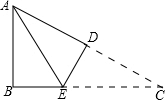 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )| A. | 4cm | B. | $\frac{3}{2}$cm | C. | $\frac{25}{8}$cm | D. | $\frac{7}{2}$cm |
 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AHF=50°,求:∠AGE的度数.
已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AHF=50°,求:∠AGE的度数.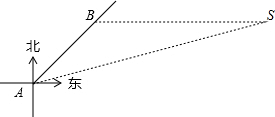 如图,一艘向东北方向航行的船,在A处观测灯塔S在船的北偏东67.5°的方向,航行6海里后到达B处,这时灯塔S恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗?为什么?(参考数据:tan22.5°≈$\frac{2}{5}$;sin22.5°≈$\frac{19}{50}$;cos22.5°≈$\frac{23}{25}$)
如图,一艘向东北方向航行的船,在A处观测灯塔S在船的北偏东67.5°的方向,航行6海里后到达B处,这时灯塔S恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗?为什么?(参考数据:tan22.5°≈$\frac{2}{5}$;sin22.5°≈$\frac{19}{50}$;cos22.5°≈$\frac{23}{25}$)