题目内容
18.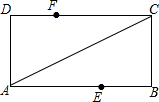 如图,矩形ABCD中,AB=2,BC=4,将矩形沿对角线AC翻折,使AB边上的点E与CD边上的点F重合,则AE的长是2.5.
如图,矩形ABCD中,AB=2,BC=4,将矩形沿对角线AC翻折,使AB边上的点E与CD边上的点F重合,则AE的长是2.5.
分析 连接EF、AF、CE,EF交AC于O,根据菱形的判定定理得到四边形AECF是菱形,得到AE=EC,设AE=x,根据勾股定理列出方程,解方程即可.
解答 解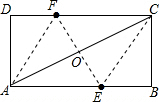 :连接EF、AF、CE,EF交AC于O,
:连接EF、AF、CE,EF交AC于O,
由翻折变换的性质可知OF=OE,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DCA=∠BAC,
在△FCO和△EAO中,
$\left\{\begin{array}{l}{∠FCO=∠EAO}\\{∠FOC=∠EOA}\\{OF=OE}\end{array}\right.$,
∴△FCO≌△EAO,
∴OA=OC,又OE=OF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形,
∴AE=EC,
设AE=x,则EC=x,BE=4-x,
在Rt△CEB中,CE2=BE2+BC2,即x2=22+(4-x)2,
解得x=2.5.
故答案为:2.5.
点评 本题考查的是翻折变换的性质和勾股定理的应用,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
13.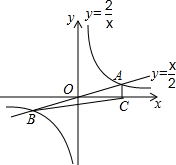 如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
 如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 1 |
3.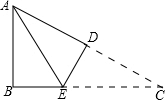 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )| A. | 4cm | B. | $\frac{3}{2}$cm | C. | $\frac{25}{8}$cm | D. | $\frac{7}{2}$cm |
 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AHF=50°,求:∠AGE的度数.
已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AHF=50°,求:∠AGE的度数.