题目内容
14.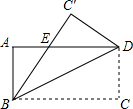 如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )
如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 2$\sqrt{3}$ |
分析 由矩形的性质和折叠的性质得出∠C′BD=∠DBC=∠BDA,可得DE=BE,设BE=DE=x,则AE=8-x.根据勾股定理得出方程,解方程即可.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DBC=∠BDA,
由折叠的性质得:∠C′BD=∠DBC,
∴∠C′BD=∠BDA,
∴DE=BE,
设BE=DE=x,则AE=8-x.
在△ABE中,由勾股定理得:
x2=42+(8-x)2.
解得:x=5,
∴BE=5.
故选:C.
点评 此题考查了矩形的性质、翻折变换的性质、等腰三角形的判定、勾股定理;熟练掌握矩形和翻折变换的性质,由勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
19.点M(-3,-5)是由N先向上平移4个单位,再向左平移3个单位而得到,则点N的坐标为( )
| A. | (0,-9) | B. | (-6,-1) | C. | (1,-2) | D. | (1,-8) |
3.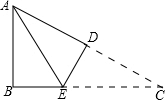 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )| A. | 4cm | B. | $\frac{3}{2}$cm | C. | $\frac{25}{8}$cm | D. | $\frac{7}{2}$cm |
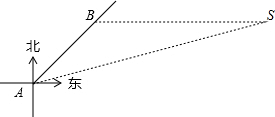 如图,一艘向东北方向航行的船,在A处观测灯塔S在船的北偏东67.5°的方向,航行6海里后到达B处,这时灯塔S恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗?为什么?(参考数据:tan22.5°≈$\frac{2}{5}$;sin22.5°≈$\frac{19}{50}$;cos22.5°≈$\frac{23}{25}$)
如图,一艘向东北方向航行的船,在A处观测灯塔S在船的北偏东67.5°的方向,航行6海里后到达B处,这时灯塔S恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗?为什么?(参考数据:tan22.5°≈$\frac{2}{5}$;sin22.5°≈$\frac{19}{50}$;cos22.5°≈$\frac{23}{25}$)