题目内容
9.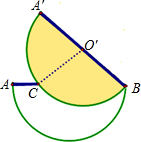 将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形,$\widehat{AB}$与直径AB交于点C,连接点C与圆心O′.
将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形,$\widehat{AB}$与直径AB交于点C,连接点C与圆心O′.(1)求$\widehat{BC}$的长;
(2)求图中下面这张半圆形纸片未被上面这张纸片重叠部分的面积S白.
分析 (1)连结BC,作O′D⊥BC于D,根据旋转变换的性质求出∠CBA′的度数,根据弧长公式计算即可;
(2)根据扇形面积公式、三角形面积公式,结合图形计算即可.
解答 解:(1)连结BC,作O′D⊥BC于D,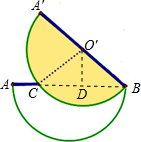
由题意得,∠CBA′=30°,
则∠BO′C=120°,O′D=$\frac{1}{2}$O′B=5,
∴$\widehat{BC}$的长为:$\frac{120×π×10}{180}$=$\frac{20}{3}π$;
(2)S白=$\frac{1}{2}$×π×102-($\frac{120×π×1{0}^{2}}{360}$-$\frac{1}{2}$×10$\sqrt{3}$×5)
=50π-$\frac{100}{3}π$+25$\sqrt{3}$
=$\frac{50}{3}$π+25$\sqrt{3}$.
点评 本题考查的是扇形面积的计算、弧长的计算、旋转变换的性质、直角三角形的性质,掌握扇形面积公式:S扇形=$\frac{n}{360}$πR2和弧长公式:l=$\frac{nπr}{180}$是解题的关键.

练习册系列答案
相关题目
3.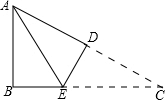 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )| A. | 4cm | B. | $\frac{3}{2}$cm | C. | $\frac{25}{8}$cm | D. | $\frac{7}{2}$cm |
17.若二元一次方程组$\left\{\begin{array}{l}{ax-2016y=2015}\\{2016x-by=2017}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,则二元一次方程组$\left\{\begin{array}{l}{a(x-y)-2016(x+y)=2015}\\{2016(x-y)-b(x+y)=2017}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{1}{2}}\end{array}\right.$ |
1.小明与父母从海口乘火车去上海,他们买到的火车票是同一排相邻的三个座位,那么小明恰好坐在父母中间的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 a、b在数轴上的位置如图所示,化简:|a+b|-2|a-b|=-3a+b.
a、b在数轴上的位置如图所示,化简:|a+b|-2|a-b|=-3a+b.