题目内容
16.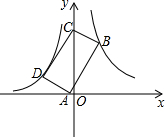 如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.
如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.(1)求点B所在双曲线的解析式.
(2)求点A的坐标.
分析 (1)将点B坐标代入y=$\frac{k}{x}$求得k的值即可;
(2)过点D作DE⊥x轴、过点B作BF⊥x轴,可得△ADE∽△BAF,由相似形性质知$\frac{DE}{AF}=\frac{AE}{BF}$=$\frac{AD}{AB}$=$\frac{1}{2}$,设点A坐标为(m,0),分别表示出AE、DE的长,进而表示出点D坐标,由点D在y=-$\frac{8}{x}$上可得关于m的方程,解方程求得m的值即可.
解答 解:(1)根据题意,将点B(3,6)代入y=$\frac{k}{x}$,解得:k=18,
故点B所在双曲线的解析式为:y=$\frac{18}{x}$;
(2)如图,过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,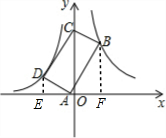
∴∠DEA=∠OFB=90°,
∴∠DAE+∠ADE=90°,
∵四边形ABCD是矩形,
∴∠DAB=90°,即∠DAE+∠BAF=90°,
∴∠ADE=∠BAF,
∴△ADE∽△BAF,
∴$\frac{DE}{AF}=\frac{AE}{BF}$=$\frac{AD}{AB}$=$\frac{1}{2}$,
设点A坐标为(m,0),B(3,6)
则AF=3-m,
∴AE=$\frac{1}{2}$BF=3,DE=$\frac{1}{2}$AF=$\frac{3-m}{2}$,
故点D的坐标为(m-3,$\frac{3-m}{2}$),
∵点D在y=-$\frac{8}{x}$上,
∴$\frac{3-m}{2}$=-$\frac{8}{m-3}$,
解得:m=-1或m=7(舍),
故点A的坐标为(-1,0).
点评 本题考查了待定系数法求函数解析式及相似三角形的判定与性质,通过相似三角形的性质表示出点D的坐标是解题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
4.已知抛物线y=-(x-m)2的顶点为A,直线l:y=$\sqrt{3}$x-$\sqrt{3}$m,其中m>0
(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
10. 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
 如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.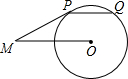 如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )
如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( ) 如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.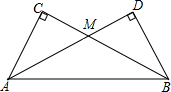 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点. 如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.
如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.