题目内容
11.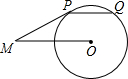 如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )
如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | π |
分析 连接OP、OQ,由切线的性质可得∠OPM=90°,易得∠POM=60°,OM=2OP,可得△POQ为正三角形,由劣弧PQ的弧长为$\frac{π}{3}$,可得OP的长,可得结果.
解答 解: 连接OP、OQ,
连接OP、OQ,
∵PM为⊙O的切线,
∴∠OPM=90°,
∵∠OMP=30°,
∴∠POM=60°,OM=2OP,
∵PQ∥OM,
∴∠OPQ=∠POM=60°,
∴△POQ为正三角形,
∴$\frac{60°•π•OP}{180°}$=$\frac{π}{3}$,
∴OP=1,
∴OM=2,
故选B.
点评 本题主要考查了切线的性质,作出恰当的辅助线“见切点,连半径”是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
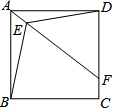 如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.
如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.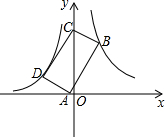 如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.
如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.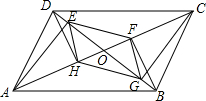 如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.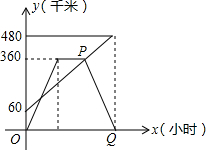 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图: 在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,如点p从O点出发1秒时,点p的坐标为(0,1)(1,0),整数点个数为2个;点p从O点出发2秒时,点p的坐标为(0,2)(2,0),(1,1),整数点个数为3个…,当P点从点O出发10秒时,可得到整数点有11个;当P点从点O出发15秒时,可得到整数点(10,5).
在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,如点p从O点出发1秒时,点p的坐标为(0,1)(1,0),整数点个数为2个;点p从O点出发2秒时,点p的坐标为(0,2)(2,0),(1,1),整数点个数为3个…,当P点从点O出发10秒时,可得到整数点有11个;当P点从点O出发15秒时,可得到整数点(10,5).