题目内容
8.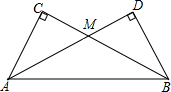 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.(1)此时MC的长度等于点M到AB的距离,请说明理由.
(2)图中除同样大小的三角尺外,你还能找出全等的三角形吗?如果能,请写出来并说明理由.
分析 (1)过点M做MN⊥AB,利用角平分线的性质以及全等三角形的性质得出答案;
(2)根据AAS定理可得出△AMC≌△BMD.
解答 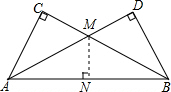 解:(1)过点M做MN⊥AB,由题意可得:∠CAD=∠DAB=30°,
解:(1)过点M做MN⊥AB,由题意可得:∠CAD=∠DAB=30°,
∵∠C=90°,MN⊥AB,
∴MC=MN(角平分线上的点到角的两边距离相等),即则MC的长度就等于点M到AB的距离;
(2)△AMC≌△BMD.
理由:在△AMC与△BMD中,
$\left\{\begin{array}{l}∠C=∠D\\∠AMC=∠BMD\\ AC=BD\end{array}\right.$,
∴△AMC≌△BMD(AAS),
点评 本题考查的是全等三角形的判定,熟知全等三角形的判定定理是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知:$\sqrt{2}$cos(x+15°)=1,则sinx的值是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
13. 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )| A. | 2$\sqrt{3}$ | B. | 3π-2$\sqrt{3}$ | C. | 3π-4$\sqrt{3}$ | D. | 3π |
2.现有五张完全相同的卡片,某同学在其中四张的正面分别写上了春节、清明节、端午节、重阳节这四个中国传统节日,在第五张的正面写上了国庆节,然后把卡片背面朝上洗匀,从中随机抽取一张卡片,则所抽取卡片正面所写节日是中国传统节日的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
3. 如图,从一艘船上测得一个灯塔的方向是北偏西47°,那么这艘船在这个灯塔的( )
如图,从一艘船上测得一个灯塔的方向是北偏西47°,那么这艘船在这个灯塔的( )
 如图,从一艘船上测得一个灯塔的方向是北偏西47°,那么这艘船在这个灯塔的( )
如图,从一艘船上测得一个灯塔的方向是北偏西47°,那么这艘船在这个灯塔的( )| A. | 南偏东47° | B. | 南偏东43° | C. | 南偏西47° | D. | 南偏西43° |
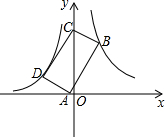 如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.
如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.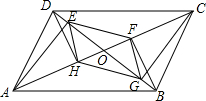 如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.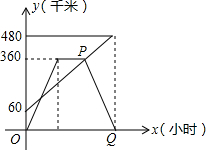 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图: