题目内容
10．
如图，在?ABCD中，点E在DC上，BE与AC相交于点F，若$\frac{DE}{EC}$=$\frac{1}{2}$，则$\frac{BF}{BE}$的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{2}{3}$ |
分析 根据CD∥AB得到$\frac{EF}{FB}$=$\frac{EC}{AB}$，由$\frac{DE}{EC}$=$\frac{2}{3}$，推出$\frac{EC}{DC}$=$\frac{EC}{AB}$=$\frac{2}{3}$，由此即可解决问题．
解答 解：∵四边形ABCD是平行四边形，
∴CD=AB，CD∥AB，
∴$\frac{EC}{AB}$=$\frac{EF}{FB}$，
∵$\frac{DE}{EC}$=$\frac{1}{2}$，
∴$\frac{EC}{CD}$=$\frac{EC}{AB}$=$\frac{2}{3}$，
∴$\frac{EF}{FB}$=$\frac{2}{3}$，
∴$\frac{BF}{BE}$=$\frac{3}{5}$．
故选A．
点评 本题考查平行四边形的性质、平行线分线段成比例定理，解题的关键是熟练掌握平行线分线段成比例定理，属于中考常考题型．
练习册系列答案
阅读快车系列答案
相关题目
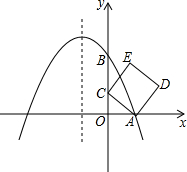如图，在平面直角坐标系中，抛物线y=ax2+bx+2与x轴交于点A（1，0），与y轴交于点B，其对称轴是x=-1，点C是y轴上一点，其纵坐标为m，连结AC，将线段AC绕点A顺时针旋转90°得到线段AD，以AC、AD为边作正方形ACED．
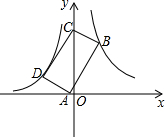如图，点B（3，6）在双曲线y=$\frac{k}{x}$（x＞0）上，点D在双曲线y=-$\frac{8}{x}$（x＜0）上，点A和点C分别在x轴和y轴上，且四边形ABCD是矩形，AB=2BC．
13．
如图，四边形ABCD是⊙O的内接四边形，∠ABC=2∠D，连接OA，OB，OC，AC，OB与AC相交于点E，若∠COB=3∠AOB，OC=2$\sqrt{3}$，则图中阴影部分面积为（ ）
如图，四边形ABCD是⊙O的内接四边形，∠ABC=2∠D，连接OA，OB，OC，AC，OB与AC相交于点E，若∠COB=3∠AOB，OC=2$\sqrt{3}$，则图中阴影部分面积为（ ）| A． | 2$\sqrt{3}$ | B． | 3π-2$\sqrt{3}$ | C． | 3π-4$\sqrt{3}$ | D． | 3π |
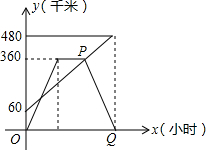甲、乙两车分别从相距480km的A、B两地相向而行，乙车比甲车先出发1小时，并以各自的速度匀速行驶，途径C地，甲车到达C地停留1小时，因有事按原路原速返回A地．乙车从B地直达A地，两车同时到达A地．甲、乙两车距各自出发地的路程y（千米）与甲车出发所用的时间x（小时）的关系如图：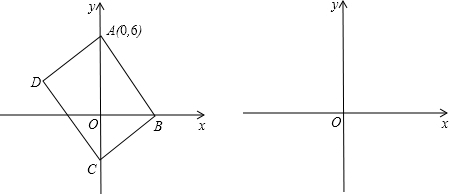
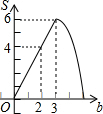
2．现有五张完全相同的卡片，某同学在其中四张的正面分别写上了春节、清明节、端午节、重阳节这四个中国传统节日，在第五张的正面写上了国庆节，然后把卡片背面朝上洗匀，从中随机抽取一张卡片，则所抽取卡片正面所写节日是中国传统节日的概率是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{5}$ |
如图，在平面直角坐标系xOy中，四边形OABC是矩形，点A（4，0），C（0，3）．直线y=$\frac{1}{2}x$由原点开始向上平移，所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点，设△OMN面积为S，那么能表示S与b函数关系的图象大致是（ ）
