题目内容
4.已知抛物线y=-(x-m)2的顶点为A,直线l:y=$\sqrt{3}$x-$\sqrt{3}$m,其中m>0(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
分析 (1)由抛物线的顶点式可知其对称轴和顶点坐标;
(2)将点A的坐标代入直线解析式即可判断.
解答 解:(1)由抛物线y=-(x-m)2可知其对称轴为x=m,顶点A的坐标为(m,0);
(2)在直线l:y=$\sqrt{3}$x-$\sqrt{3}$m中,
当x=m时,y=$\sqrt{3}$m-$\sqrt{3}$m=0,
故点A(m,0)在直线l上.
点评 本题主要考查二次函数的性质,利用解析式化为y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )| A. | 2$\sqrt{3}$ | B. | 3π-2$\sqrt{3}$ | C. | 3π-4$\sqrt{3}$ | D. | 3π |
 已知∠BAC=90°,四边形ADEF是正方形且边长为1,则$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值为1+$\frac{\sqrt{2}}{4}$,简述理由(可列式):$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.
已知∠BAC=90°,四边形ADEF是正方形且边长为1,则$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值为1+$\frac{\sqrt{2}}{4}$,简述理由(可列式):$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.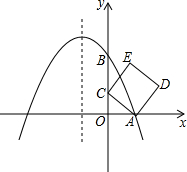 如图,在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交于点A(1,0),与y轴交于点B,其对称轴是x=-1,点C是y轴上一点,其纵坐标为m,连结AC,将线段AC绕点A顺时针旋转90°得到线段AD,以AC、AD为边作正方形ACED.
如图,在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交于点A(1,0),与y轴交于点B,其对称轴是x=-1,点C是y轴上一点,其纵坐标为m,连结AC,将线段AC绕点A顺时针旋转90°得到线段AD,以AC、AD为边作正方形ACED.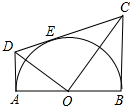 如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )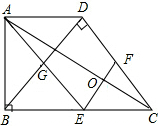 已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.
已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.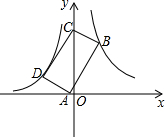 如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.
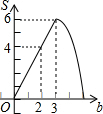
如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC. 如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=$\frac{1}{2}x$由原点开始向上平移,所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是( )
如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=$\frac{1}{2}x$由原点开始向上平移,所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是( )