题目内容
11.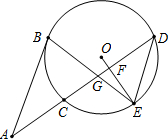 如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.
如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.(1)求证:AB=AG;
(2)若DG=DE,求证:GB2=GC•GA;
(3)在(2)的条件下,若tanD=$\frac{3}{4}$,EG=$\sqrt{10}$,求⊙O的半径.
分析 (1)由AB为⊙O切线,得到OB⊥AB,根据垂径定理得到OE⊥CD,根据等腰三角形的性质得到∠OBG=∠OEG,等量代换得到∠ABG=∠BGA,即可得到结论;
(2)根据等腰三角形的性质得到∠DGE=∠DEG,根据已知条件得到∠A=∠D,等量代换得到∠GBC=∠A,推出△GBC∽△GAB,根据相似三角形的性质即可得到结论;
(3)在Rt△DEF中,tanD=$\frac{EF}{DF}=\frac{3}{4}$,设EF=3x,则DF=4x,由勾股定理得DE=5x,根据勾股定理列方程得到x=1,设⊙O半径为r,根据勾股定理列方程即可得到结论.
解答  (1)证明:如图,连接OB.
(1)证明:如图,连接OB.
∵AB为⊙O切线,
∴OB⊥AB,
∴∠ABG+∠OBG=90°,
∵点E为$\widehat{DC}$的中点,
∴OE⊥CD,
∴∠OEG+∠FGE=90°,
又∵OB=OE,
∴∠OBG=∠OEG,
∴∠ABG=∠FGE,
∵∠BGA=∠FGE,
∴∠ABG=∠BGA,
∴AB=AG;
(2)证明:连接BC,
∵DG=DE,
∴∠DGE=∠DEG,
由(1)得∠ABG=∠BGA,
又∵∠BGA=∠DGE,
∴∠A=∠D,
∵∠GBC=∠D,
∴∠GBC=∠A,
∵∠BGC=∠AGB,
∴△GBC∽△GAB,
∴$\frac{GB}{AB}=\frac{GC}{GB}$,
∴GB2=GC•GA;
(3)连接OD,在Rt△DEF中,tanD=$\frac{EF}{DF}=\frac{3}{4}$,
∴设EF=3x,则DF=4x,由勾股定理得DE=5x,
∵DG=DE,
∴DG=5x,
∴GF=DG-DF=x.
在Rt△EFG中,由勾股定理得GF2+EF2=EG2,
即(3x)2+x2=($\sqrt{10}$)2,解得x=1,
设⊙O半径为r,在Rt△ODF中,OD=r,OF=r-3x=r-3,DF=4x=4,
由勾股定理得:OF2+FD2=OD2,即(r-3)2+(4)2=r2,
解得r=$\frac{25}{6}$,
∴⊙O的半径为$\frac{25}{6}$.
点评 本题考查了切线的性质,相似三角形的判定和性质,勾股定理,等腰三角形的性质,垂径定理,连接BC构造相似三角形是解决(2)的关键.

 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
| A. | S和C | B. | S和a | C. | C和a | D. | S,C,a |
 如图,从一艘船上测得一个灯塔的方向是北偏西47°,那么这艘船在这个灯塔的( )
如图,从一艘船上测得一个灯塔的方向是北偏西47°,那么这艘船在这个灯塔的( )| A. | 南偏东47° | B. | 南偏东43° | C. | 南偏西47° | D. | 南偏西43° |
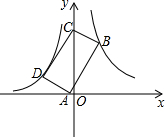 如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.
如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC. 如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=$\frac{1}{2}x$由原点开始向上平移,所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是( )
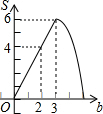
如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=$\frac{1}{2}x$由原点开始向上平移,所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是( )


 在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,如点p从O点出发1秒时,点p的坐标为(0,1)(1,0),整数点个数为2个;点p从O点出发2秒时,点p的坐标为(0,2)(2,0),(1,1),整数点个数为3个…,当P点从点O出发10秒时,可得到整数点有11个;当P点从点O出发15秒时,可得到整数点(10,5).
在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,如点p从O点出发1秒时,点p的坐标为(0,1)(1,0),整数点个数为2个;点p从O点出发2秒时,点p的坐标为(0,2)(2,0),(1,1),整数点个数为3个…,当P点从点O出发10秒时,可得到整数点有11个;当P点从点O出发15秒时,可得到整数点(10,5).