题目内容
3.用反证法证明真命题“四边形中至少有一个角不小于90°”时,应假设( )| A. | 四边形中没有一个角不小于90° | B. | 四边形中至少有两个角不小于90° | ||
| C. | 四边形中四个角都不小于90° | D. | 四边形中至多有一个角不小于90° |
分析 至少有一个角不小于90°的反面是每个角都不小于90°,据此即可假设.
解答 解:用反证法证明:在四边形中,至少有一个角不小于90°,应先假设:四边形中没有一个角不小于90°.
故选A.
点评 本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
13.若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=$\frac{1}{x}$图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
| A. | x1<x2<x3 | B. | x1<x3<x2 | C. | x2<x1<x3 | D. | x2<x3<x1 |
14.一个正多边形形的内角和是1440°,则它的每个外角的度数是( )
| A. | 30° | B. | 36° | C. | 45° | D. | 60° |
8.若点P(m+3,m-1)在x轴上,则P点的坐标为( )
| A. | (0,-4) | B. | (4,0) | C. | (0,4) | D. | (-4,0) |
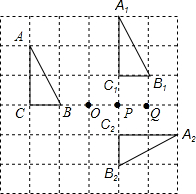 在如图所示的方格纸中,△ABC,△A1B1C1,△A2B2C2的顶点及O、P、Q都在格点上(每个小方格的顶点叫格点)
在如图所示的方格纸中,△ABC,△A1B1C1,△A2B2C2的顶点及O、P、Q都在格点上(每个小方格的顶点叫格点)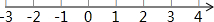
 如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(-1,m).
如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(-1,m). 在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm,则OB=$\sqrt{73}$cm.
在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm,则OB=$\sqrt{73}$cm.