题目内容
13．（1）解方程；$\frac{3}{2x-2}$+$\frac{1}{1-x}$=3（2）先化简：（$\frac{a+3}{a-2}+\frac{1}{2-a}$）÷$\frac{{a}^{2}-4}{3}$请在2和3中选择一个合适的数代入求值．
分析 （1）先把分式方程化为整式方程求出x的值，再代入最减公分母进行检验即可；
（2）先算括号里面的，再算除法，最后选出x的值代入进行计算即可．
解答 解：（1）去分母得，3-2=3（2x-2），解得x=$\frac{7}{6}$，
经检验x=$\frac{7}{6}$是原分式方程的解；
（2）原式=$\frac{a+3-1}{a-2}$•$\frac{3}{（a+2）（a-2）}$
=$\frac{a+2}{a-2}$•$\frac{3}{（a+2）（a-2）}$
=$\frac{3}{（a-2）^{2}}$，
当a=3时，原式=3．
点评 本题考查的是分式的化简求值，分式求值题中比较多的题型主要有三种：转化已知条件后整体代入求值；转化所求问题后将条件整体代入求值；既要转化条件，也要转化问题，然后再代入求值．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
4．某校为了选拔学生参加“汉字听写大赛”，对九年级一班、二班各10名学生进行汉字听写测试，计分采用10分制（得分均取整数），成绩达到6分或6分以上为及格、达到9分或10分以上为优秀．这20位同学的成绩与统计数据如表：
（1）在表中，a=8，b=7.5；
（2）有人说二班的及格率、优秀率高于一班，所以二班的成绩比一班好，但也有人坚持认为一班成绩比二班好，请你给出支持一班成绩好的两条理由；
（3）若从这两班获满分的同学中随意抽1名同学参加“汉字听写大赛”，求参赛同学恰好是一班同学的概率．
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
| 一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 | 7.6 | 8 | a | 3.82 | 70% | 30% |
| 二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 | b | 7.5 | 10 | 4.94 | 80% | 40% |
（2）有人说二班的及格率、优秀率高于一班，所以二班的成绩比一班好，但也有人坚持认为一班成绩比二班好，请你给出支持一班成绩好的两条理由；
（3）若从这两班获满分的同学中随意抽1名同学参加“汉字听写大赛”，求参赛同学恰好是一班同学的概率．
1．下列命题：
①平行于同一直线的两条直线平行；
②在同一平面内，垂直于同一直线的两条直线平行；
③过一点有且只有一条直线与已知直线平行；
④在同一平面内，过一点有且只有一条直线与已知直线垂直．
其中，真命题共有（ ）
①平行于同一直线的两条直线平行；
②在同一平面内，垂直于同一直线的两条直线平行；
③过一点有且只有一条直线与已知直线平行；
④在同一平面内，过一点有且只有一条直线与已知直线垂直．
其中，真命题共有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．下列二次根式，最简二次根式是（ ）
| A． | $\sqrt{\frac{1}{5}}$ | B． | $\sqrt{0.5}$ | C． | $\sqrt{5}$ | D． | $\sqrt{50}$ |
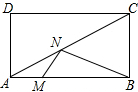如图，在矩形ABCD中，AB=4，AD=2，点M是AB上一动点，点N是对角线AC上一动点，则MN+BN的最小值为$\frac{16}{5}$．
2．下列四个图形中，不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
3．一次函数y=-2x-3的图象与y轴的交点坐标是（ ）
| A． | （3，0） | B． | （0，3） | C． | （-3，0） | D． | （0，-3） |