题目内容
3.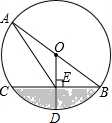 如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.
如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.(1)求证:OE=DE;
(2)若OE=2,求图中阴影部分的面积.
分析 (1)连结OC,OD,先证明△OCD是等边三角形,再根据三线合一的性质即可证明OE=DE;
(2)图中阴影部分的面积=扇形OBC的面积-三角形OBC的面积,根据扇形的面积公式和三角形的面积公式计算即可求解..
解答  (1)证明:连结OC,OD,
(1)证明:连结OC,OD,
∵$\widehat{CD}$=60°,OC=OD,
∴△OCD是等边三角形,
∵OD⊥BC,
∴OE=DE;
(2)∵OE=2,
∴OD=4,
阴影部分的面积=扇形OBC的面积-三角形OBC的面积
=$\frac{60×2}{360}$×π×42-$\frac{1}{2}$×2×2tan60°×2
=$\frac{16}{3}$π-4$\sqrt{3}$.
答:图中阴影部分的面积是$\frac{16}{3}$π-4$\sqrt{3}$.
点评 考查了扇形面积、三角形的面积的计算,正确证明△OCD是等边三角形是关键.

练习册系列答案
相关题目
18. 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D作⊙O的切线交AC于E
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D作⊙O的切线交AC于E
(1)求证:DE⊥AC;
(2)连OC交DE于F,若AE=2,DE=3,求$\frac{DF}{EF}$的值.
 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D作⊙O的切线交AC于E
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D作⊙O的切线交AC于E(1)求证:DE⊥AC;
(2)连OC交DE于F,若AE=2,DE=3,求$\frac{DF}{EF}$的值.
8.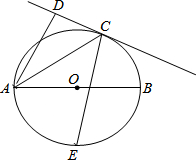 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )| A. | 7$\sqrt{2}$ | B. | 7$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
15.一个等腰三角形的周长为15cm,一腰上的中线把周长分为两部分,这两部分的差为6cm,则腰长为( )
| A. | $\frac{3}{2}$cm | B. | $\frac{3}{2}$cm或7cm | C. | 7cm | D. | 7cm或1cm |
 如图,⊙O为△ABC的外接圆,AB为⊙O的直径,延长AB到点E,连结EC,且∠BCE=∠BAC.
如图,⊙O为△ABC的外接圆,AB为⊙O的直径,延长AB到点E,连结EC,且∠BCE=∠BAC.