题目内容
15.一个等腰三角形的周长为15cm,一腰上的中线把周长分为两部分,这两部分的差为6cm,则腰长为( )| A. | $\frac{3}{2}$cm | B. | $\frac{3}{2}$cm或7cm | C. | 7cm | D. | 7cm或1cm |
分析 根据题意设AB=AC=x,则BC=15-2x,AD=CD=$\frac{1}{2}$x,得出AB+AD=x+$\frac{1}{2}$x=$\frac{3}{2}$x,BC+CD=15-2x+$\frac{1}{2}$x;分两种情况:①(AB+AD)-(BC+CD)=6厘米时;②当(BC+CD)-(AB+AD)=6厘米时;由题意得出方程,解方程即可.
解答 解:如图所示: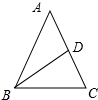
∵BD是腰AC的中线,
∴AD=CD,
设AB=AC=x,
则BC=15-2x,AD=CD=$\frac{1}{2}$x,
∴AB+AD=x+$\frac{1}{2}$x=$\frac{3}{2}$x,BC+CD=15-2x+$\frac{1}{2}$x;
∵中线BD把△ABC的周长分为两部分之差为6厘米,
∴分两种情况:
①(AB+AD)-(BC+CD)=6厘米时,
$\frac{3}{2}$x-(15-$\frac{3}{2}$x)=6,
解得:x=7,
∴15-2x=2,
∵2+7>7,
∴符合题意,
∴AB=AC=7厘米;
②当(BC+CD)-(AB+AD)=6厘米时,
(15-$\frac{3}{2}$x)-$\frac{3}{2}$x=6,
解得:x=3,
∴15-2x=9,
∵3+3<9,
∴不符合题意,
综上所述:腰长为7厘米,
故选C.
点评 本题考查了等腰三角形的性质、三角形的三边关系;熟练掌握等腰三角形的性质和三角形的三边关系,并能进行推理计算是解决问题的关键;本题需要分类讨论.

练习册系列答案
相关题目
10.3-2与32的关系为( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 和为零 | D. | 绝对值相等 |
 )2+
)2+ =0,则∠C的度数为________.
=0,则∠C的度数为________. 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于F.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于F.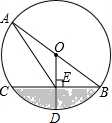 如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.
如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.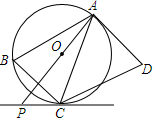 如图,四边形ABCD是平行四边形,⊙O是△ABC的外接圆,AD与⊙O相切于点A,AO的延长线与过点C的直线相交于点P,且∠PCB=∠ACD.
如图,四边形ABCD是平行四边形,⊙O是△ABC的外接圆,AD与⊙O相切于点A,AO的延长线与过点C的直线相交于点P,且∠PCB=∠ACD.