题目内容
 如图所示,已知CD∥EF,∠1+∠2=∠ABC,试判断AB与GF的位置关系,并说明理由.
如图所示,已知CD∥EF,∠1+∠2=∠ABC,试判断AB与GF的位置关系,并说明理由.考点:平行线的判定与性质
专题:计算题
分析:过点B作BM∥CD,交GF于M,反向延长MB取点H,由BM与CD平行,得到一对内错角相等,由∠ABC=∠CBH+∠ABH及∠1+∠2=∠ABC等量代换得到∠1=∠ABH,由平行于同一条直线的两直线平行得到BM与EF平行,利用两直线平行同位角相等得到∠BMG=∠1,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证.
解答: 证明:过点B作BM∥CD,交GF于M,反向延长MB取点H,
证明:过点B作BM∥CD,交GF于M,反向延长MB取点H,
∵BM∥CD,
∴∠2=∠CBH,
∵∠ABC=∠CBH+∠ABH,
∴∠ABC=∠2+∠ABH,
∵∠ABC=∠1+∠2,
∴∠1=∠ABH,
∵CD∥EF,
∴BM∥EF,
∴∠BMG=∠1,
∴∠ABH=∠BMG,
∴AB∥GF.
 证明:过点B作BM∥CD,交GF于M,反向延长MB取点H,
证明:过点B作BM∥CD,交GF于M,反向延长MB取点H,∵BM∥CD,
∴∠2=∠CBH,
∵∠ABC=∠CBH+∠ABH,
∴∠ABC=∠2+∠ABH,
∵∠ABC=∠1+∠2,
∴∠1=∠ABH,
∵CD∥EF,
∴BM∥EF,
∴∠BMG=∠1,
∴∠ABH=∠BMG,
∴AB∥GF.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
相关题目
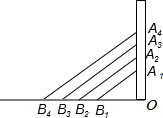 斜拉桥是我国流行的桥型之一,大跨径斜拉桥已居世界第一.如图,OA1=A1A2=A2A3=A3A4,OB1=B1B2=B2B3=B3B4,如果最长的钢索A4B4=80cm,那么钢索A2B2、A1B1的长分别是( )
斜拉桥是我国流行的桥型之一,大跨径斜拉桥已居世界第一.如图,OA1=A1A2=A2A3=A3A4,OB1=B1B2=B2B3=B3B4,如果最长的钢索A4B4=80cm,那么钢索A2B2、A1B1的长分别是( )| A、60m,40m |
| B、60m,30m |
| C、40m,20m |
| D、40m,10m |
 如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )
如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )| A、14 | B、18 | C、24 | D、48 |
 如图,在△ABC中,∠B=30°,AB=AC=2
如图,在△ABC中,∠B=30°,AB=AC=2 在△ABC中,∠A=60°,以BC为直径作圆O交AC于点D,交AB于点E,连接DE,BD,CE.试证明:△ADE∽△ABC.
在△ABC中,∠A=60°,以BC为直径作圆O交AC于点D,交AB于点E,连接DE,BD,CE.试证明:△ADE∽△ABC.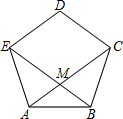 正五边形ABCDE的对角线AC、BE相交于点M.
正五边形ABCDE的对角线AC、BE相交于点M.