题目内容
 如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )
如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )| A、14 | B、18 | C、24 | D、48 |
考点:勾股定理
专题:
分析:阴影部分面积可以看成是以AC、BC为直径的两个半圆的面积加上一个直角三角形ABC的面积减去一个以AB为直径的半圆的面积.
解答:解:S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC-直径为AB的半圆的面积
=
π(
)2+
π(
)2+
AC×BC-
π(
)2
=
π(AC)2+
π(BC)2-
π(AB)2+
AC×BC
=
π(AC2+BC2-AB2)+
AC×BC
=
AC×BC
=
×6×8
=24.
故选:C.
=
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| 2 |
=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
=
| 1 |
| 8 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=24.
故选:C.
点评:此题主要考查了扇形面积的计算公式,阴影部分的面积可以看作是几个规则图形的面积的和或差.

练习册系列答案
相关题目
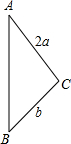 如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )
如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )| A、2πa2 |
| B、πab |
| C、3πa2+πab |
| D、πa(2a+b) |
设x3-3
x2+6x-2
-8=0,则x5-41x2+1的值为( )
| 2 |
| 2 |
A、13-
| ||
B、-13+
| ||
| C、-13 | ||
| D、13 |
 如图,A,B,C在同一直线上,△ABD,△BCE都是等边三角形,AE交BD于点E,DC交BE于点G,求证:BF=BG.
如图,A,B,C在同一直线上,△ABD,△BCE都是等边三角形,AE交BD于点E,DC交BE于点G,求证:BF=BG.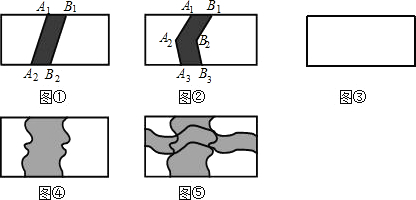
 如图所示,已知CD∥EF,∠1+∠2=∠ABC,试判断AB与GF的位置关系,并说明理由.
如图所示,已知CD∥EF,∠1+∠2=∠ABC,试判断AB与GF的位置关系,并说明理由.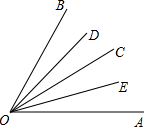 如图,已知∠AOB=60°,OC是∠AOB的平分线,OD、OE分别平分∠BOC和∠AOC.
如图,已知∠AOB=60°,OC是∠AOB的平分线,OD、OE分别平分∠BOC和∠AOC.