题目内容

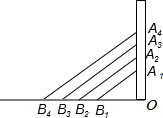斜拉桥是我国流行的桥型之一，大跨径斜拉桥已居世界第一．如图，OA1=A1A2=A2A3=A3A4，OB1=B1B2=B2B3=B3B4，如果最长的钢索A4B4=80cm，那么钢索A2B2、A1B1的长分别是（　　）
A、60m，40m
B、60m，30m
C、40m，20m
D、40m，10m
考点：三角形中位线定理
专题：应用题
分析：先根据OA1=A1A2=A2A3=A3A4，OB1=B1B2=B2B3=B3B4得出相似三角形，再由相似三角形的对应边成比例即可得出结论．
解答：解：∵OA1=A1A2=A2A3=A3A4，OB1=B1B2=B2B3=B3B4，
∴A1，A2，A3是线段OA4的四等分点，B1，B2，B3是线段OB4的四等分点，
∴△OA1B1∽△OA4B4∽△OA2B2，
∴
OA1
OA4
=
A1B1
A4B4
=
1
4
，
OA2
OA4
=
A2B2
A4B4
=
1
2
，
∵A4B4=80cm，
∴
A1B1
80
=
1
4
，
A2B2
80
=
1
2
，
解得A1B1=20cm，A2B2=40cm．
故选C．
点评：本题考查的是三角形中位线定理及相似三角形的判定定理，熟知三角形的中位线平行于第三边，并且等于第三边的一半是解答此题的关键．
练习册系列答案
相关题目
化简：
42
=
 
．
直线y=kx+4（k≠0）与y=-2x+1交于点B，若S△ABC=
3
2
．
（1）求△ABC的周长．
（2）若点P在直线AE上，△PAC是等腰直角三角形，求P点坐标．
如图，AD是△ABC的BC边上的中线，若AB=2，AC=1，求AD的取值范围．
如图①，将线段A1A2向右平移1厘米到B1B2，得到封闭图形A1A2B1B2（即阴影部分），在图②中，将折线A1A2A3向右平移1厘米到B1B2B3，得到封闭图形A1A2A3B1B2B3（即阴影部分）．
（1）在图③中，请你类似地画一条有两个折点的折线，同样向右平移1厘米，从而得到一个封闭图形，并用阴影表示（作出对应点字母的标注）；
（2）请你分别写出上述三个图形中除去阴影部分后剩余部分的面积（设图①图②图③长方形长均为6厘米，宽均为3厘米）．S1=
 
平方厘米，S2=
 
平方厘米，S3=
 
平方厘米；
（3）联想与探索：如图④，在一块长方形草地上，为了方便劳动，有一条弯曲的小路（小路任何地方的水平宽度都是2米），长方形草的长为32米，宽为20米，请你求出空白部分表示的草地S4面积是多少平方米？
（4）联想与探索：若在第（3）小题中图④的草地的基础上又有一条横向的弯曲小路如图⑤，（横向小路任何地方的宽度都是1米），长方形草地的长为32米，宽为20米．请你求出空白部分表示的草地S5面积是多少平方米？
如图，在Rt△ABC中，已知∠ACB=90°，AC=m，∠BAC=α，求Rt△ABC的面积．
盒中有x枚黑棋和y枚白棋，这些棋除颜色外无其他差别．
（1）从盒中随机取出一枚棋子，如果它是黑棋的概率是
3
8
，写出表示x和y关系的表达式．
（2）往盒中再放进10枚黑棋，取得黑棋的概率变为
1
2
，求x和y的值．
如图所示，已知CD∥EF，∠1+∠2=∠ABC，试判断AB与GF的位置关系，并说明理由．
小王在一次做加减消元法的练习结束之后，将
2x+3y-5=0
x-2y+8=0
中第二个方程的两边任意乘上一个数，与第一个方程的两边分别相加，发现有一组x、y的值总是所得方程的解，连试了几次都是这样．因此他得到了一个猜想：设k是任意一个数，则方程2x+3y-5+k（x-2y+8）=0总有一个解是不变的．请找出这个固定的解，并验证、说明这个猜想的正确性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网