题目内容
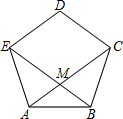 正五边形ABCDE的对角线AC、BE相交于点M.
正五边形ABCDE的对角线AC、BE相交于点M.(1)求证:四边形CDEM是菱形;
(2)设ME2=BE•BM,若AB=4,求BE的长.
考点:相似三角形的判定与性质,菱形的判定
专题:
分析:(1)证明∠D+∠DCA=180°,得到DE∥AC;同理可证DC∥BE,即可解决问题.
(2)证明△ABE∽△MAB,得到AB2=BE•BM;证明ME=AB=4,BM=BE-4,得到BE(BE-4)=16,解方程即可解决问题.
(2)证明△ABE∽△MAB,得到AB2=BE•BM;证明ME=AB=4,BM=BE-4,得到BE(BE-4)=16,解方程即可解决问题.
解答: 解:(1)∵五边形ABCDE是正五边形,
解:(1)∵五边形ABCDE是正五边形,
∴∠D=
×
×360°=108°,∠DCA=
×
×360°=72°,
∴∠D+∠DCA=180°,
∴DE∥AC;同理可证DC∥BE,
∴四边形DEMC为平行四边形,而DE=DC,
∴四边形CDEM是菱形.
(2))∵五边形ABCDE是正五边形,
∴∠AEB=
×
×360°=36°,∠EAM=
×
×360°=72°;
同理可求∠BAC=∠ABE=36°,
∴△ABE∽△MAB,
∴AB:BE=BM:AB,
∴AB2=BE•BM;
∵ME2=BE•BM,
∴ME=AB=4,BM=BE-4,
∴BE(BE-4)=16,
解得:BE=2+2
或2-2
(舍去).
 解:(1)∵五边形ABCDE是正五边形,
解:(1)∵五边形ABCDE是正五边形,∴∠D=
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
∴∠D+∠DCA=180°,
∴DE∥AC;同理可证DC∥BE,
∴四边形DEMC为平行四边形,而DE=DC,
∴四边形CDEM是菱形.
(2))∵五边形ABCDE是正五边形,
∴∠AEB=
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
同理可求∠BAC=∠ABE=36°,
∴△ABE∽△MAB,
∴AB:BE=BM:AB,
∴AB2=BE•BM;
∵ME2=BE•BM,
∴ME=AB=4,BM=BE-4,
∴BE(BE-4)=16,
解得:BE=2+2
| 5 |
| 5 |
点评:该题主要考查了相似三角形的判定、菱形的判定等几何知识点的应用问题;解题的关键是牢固掌握定理内容,灵活运用有关定理来分析、解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设x3-3
x2+6x-2
-8=0,则x5-41x2+1的值为( )
| 2 |
| 2 |
A、13-
| ||
B、-13+
| ||
| C、-13 | ||
| D、13 |
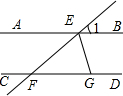 如图,AB∥CD,EF交AB、CD于点E、F、EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )
如图,AB∥CD,EF交AB、CD于点E、F、EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )| A、20° | B、40° |
| C、70° | D、110° |
 如图所示,已知CD∥EF,∠1+∠2=∠ABC,试判断AB与GF的位置关系,并说明理由.
如图所示,已知CD∥EF,∠1+∠2=∠ABC,试判断AB与GF的位置关系,并说明理由. 如图,已知直线AB与点M,N,求作一点P,使点P在直线AB上,且∠MPA=∠NPB.
如图,已知直线AB与点M,N,求作一点P,使点P在直线AB上,且∠MPA=∠NPB.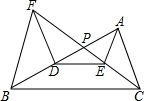 如图,在△ABC中,点D是AB上一点,E是△ABC内一点,DE∥BC,过点D作AC的平行线交CE的延长线于点F,CF与AB交于P,求证:BF∥AE.
如图,在△ABC中,点D是AB上一点,E是△ABC内一点,DE∥BC,过点D作AC的平行线交CE的延长线于点F,CF与AB交于P,求证:BF∥AE.