Question

如图，在△ABC中，∠B=30°，AB=AC=2

3

，圆A的半径1，点O在BC边上运动（与点B，C不重合），设BO=x，△AOC的面积是y．
（1）求y关于x的函数关系式，并写出自变量x的取值范围；
（2）以点O为圆心，OB的长为半径作圆，求当⊙O与⊙A相切时，△AOC的面积．

Answer 1

考点：相切两圆的性质

专题：

分析：（1）如图，作辅助线；首先求出AD、BD的长度，即可解决问题．
（2）当⊙O与⊙A相切时，运用勾股定理求出BO的值，即可解决问题．

解答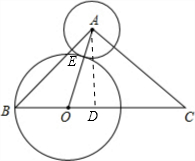：解：如图，过点A作AD⊥BC于点D；
∵AB=AC=2

3

，
∴BD=CD=

3

；
∵∠B=30°，
∴AD=

3

，BD=CD=3．
（1）∵BO=x，
∴CO=6-x，
∴y=

1

2

（6-x）×

3

=-

3

2

x+3

3

，
自变量x的取值范围是0＜x＜6．
（2）当⊙O与⊙A相切时，
AO=x+1，DO=3-x；由勾股定理得：
(x+1)2=(3-x)2+(

3

)2，
解得：x=

11

8

，
∴CO=6-

11

8

=

37

8

，
此时△AOC的面积=

1

2

×

37

8

×

3

=

37 3

16

．

点评：该题主要考查了相切两圆的性质及其应用问题；解题的关键是作辅助线；对综合的分析问题解决问题的能力提出了较高的要求．