题目内容
12.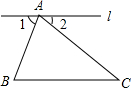 如图,点A在直线l上,如果∠B=75°,∠C=43°,若l∥BC,则∠BAC=62°.
如图,点A在直线l上,如果∠B=75°,∠C=43°,若l∥BC,则∠BAC=62°.
分析 由平行线的性质得出内错角相等,求出∠1与∠2的度数,再由平角的定义即可得出结果.
解答 解:∵l∥BC,
∴∠1=∠B=75°,∠2=∠C=43°,
∴∠BAC=180°-∠1-∠2=180°-75°-43°=62°.
故答案为:62°.
点评 本题考查了平行线的性质、平角的定义;熟记两直线平行,内错角相等是解决问题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
2.点D、E、F分别在△ABC的三边BC、AB、AC上,且AD、BF、CE相交于一点M,若$\frac{AB}{BE}+\frac{AC}{CF}=5$,则$\frac{AM}{MD}$=( )
| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
17.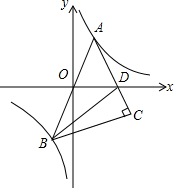 如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )
如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )
 如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )
如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
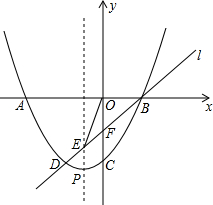 如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.
如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.
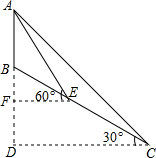 如图,山顶上有一信号塔AB,山坡BC的坡度为i=1:$\sqrt{3}$,现在为了测量塔高AB,测量人员选择山脚C处为一侧量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.
如图,山顶上有一信号塔AB,山坡BC的坡度为i=1:$\sqrt{3}$,现在为了测量塔高AB,测量人员选择山脚C处为一侧量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB. 如图,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM、ON交于A、B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,且∠MON=60°.
如图,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM、ON交于A、B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,且∠MON=60°.