题目内容
6. 如图,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM、ON交于A、B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,且∠MON=60°.
如图,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM、ON交于A、B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,且∠MON=60°.(1)求∠APB的度数;
(2)若OP=4,连接AB并求△AOB的面积.
分析 (1)由已知条件得到$\frac{OB}{OP}=\frac{OP}{OA}$,由于∠BOP=∠AOP,得到△PBO∽△AOP,根据相似三角形的性质得到∠OBP=∠OPA,根据等量代换即可得到结论;
(2)如图,连接AB,过点A作AH⊥OB,根据OA×OB=OP2=16,由于sin∠AOH=$\frac{AH}{OA}$,得到AH=OAsin∠AOH,等量代换即可得到结论.
解答 解:(1)∵OA•OB=OP2,
∴$\frac{OB}{OP}=\frac{OP}{OA}$,
∵∠BOP=∠AOP,
∴△PBO∽△AOP,
∴∠OBP=∠OPA,
∵∠MON=60°,
∴∠BOP=30°,
∴∠OBP+∠BPO=180°-30°=150°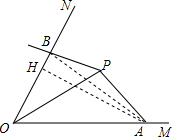
∴∠APB=∠BPO+∠APO=150°;
(2)如图,连接AB,过点A作AH⊥OB,
∵OP=4,
∴OA×OB=OP2=16,
在Rt△AOH中,∠AHO=90°,
∴sin∠AOH=$\frac{AH}{OA}$,
∴AH=OAsin∠AOH,
∴S△AOB=$\frac{1}{2}$OB×AH=$\frac{1}{2}$OB×OA×sin60°=$\frac{1}{2}$×OP2×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$.
点评 本题考查了相似三角形的判定和性质,三角形的面积的计算,三角函数的定义,得到S△AOB=$\frac{1}{2}$OB×OA×sin60°是解题的关键.

练习册系列答案
相关题目
11.已知一次函数y=(1-3m)x+1,若y随x的增大而减小,则m的取值范围是( )
| A. | m<$\frac{1}{3}$ | B. | m<-$\frac{1}{3}$ | C. | m>$\frac{1}{3}$ | D. | m>-$\frac{1}{3}$ |
18.下列运算正确的是( )
| A. | x5•x=x5 | B. | x5-x2=x3 | C. | (-y)2 (-y)7=y9 | D. | -y3•(-y)7=y10 |
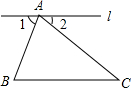 如图,点A在直线l上,如果∠B=75°,∠C=43°,若l∥BC,则∠BAC=62°.
如图,点A在直线l上,如果∠B=75°,∠C=43°,若l∥BC,则∠BAC=62°.
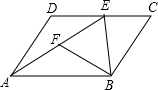 如图,在?ABCD中,过点B作BE⊥DC于点E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在?ABCD中,过点B作BE⊥DC于点E,连接AE,F为AE上一点,且∠BFE=∠C.