题目内容
15.先化简,再求值:已知m=$\frac{4}{\sqrt{5}-1}$,求$\frac{{m}^{2}-5m+6}{{m}^{2}-3m}$÷$\frac{m-2}{{m}^{2}}$的值.分析 先化简题目中的式子,然后将m的值代入即可解答本题.
解答 解:$\frac{{m}^{2}-5m+6}{{m}^{2}-3m}$÷$\frac{m-2}{{m}^{2}}$
=$\frac{(m-2)(m-3)}{m(m-3)}•\frac{{m}^{2}}{m-2}$
=m,
当m=$\frac{4}{\sqrt{5}-1}$时,原式=$\frac{4}{\sqrt{5}-1}=\sqrt{5}+1$.
点评 本题考查分式的化简求值、分母有理化,解答本题的关键是明确分式化简求值的方法、会分母有理化的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知方程3x-2y=5,把它变形为用含x的代数式表示y,正确的是( )
| A. | $y=\frac{3x-5}{2}$ | B. | $y=\frac{3x+5}{2}$ | C. | $y=\frac{-3x+5}{2}$ | D. | $y=\frac{-3x-5}{2}$ |
5.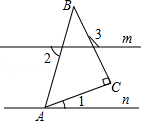 如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )
如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )
 如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )
如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
 如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )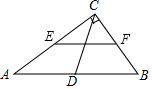 如图,在直角三角形ABC中,∠ACB=90°,D,E,F分别是AB,AC,BC的中点,若CD=5,则EF的长为5.
如图,在直角三角形ABC中,∠ACB=90°,D,E,F分别是AB,AC,BC的中点,若CD=5,则EF的长为5.