题目内容
4.已知正三角形A1B1C1的边长为a分别以这个三角形的三边中点为顶点作一个三角形,记为△A2B2C2,再以△A2B2C2各边中点为顶点做三角形记为△A3B3C3,…依次做下去,则△AnBnCn的周长为$\frac{3a}{{2}^{n-1}}$.分析 根据三角形中位线定理知,△A2B2C2的各边的边长是△A1B1C1的各边边长的$\frac{1}{2}$,△A3B3C3是,△A2B2C2的各边的边长的$\frac{1}{2}$,…,找出规律即可得出结论.
解答 解:等边△A1B1C1的边长为a,
∴等边△A1B1C1的周长为3a.
∵A2、B2分别是边A1B1、B1C1的中点,
∴A2B2是△A1B1C1的中位线,
∴A2B2=$\frac{1}{2}$A1B1.
同理,A2C2=$\frac{1}{2}$A1C1,C2B2=$\frac{1}{2}$C1B1.
∴△A2B2C2的周长=$\frac{1}{2}$等边△A1B1C1的周长=$\frac{3a}{2}$.
同理,△A3B3C3的周长=$\frac{1}{2}$△A2B2C2的周长=$\frac{3a}{{2}^{2}}$等边△A1B1C1的周长.
…,
∴△AnBnCn的周长=$\frac{1}{{2}^{n-1}}$△A1B1C1的周长=$\frac{3a}{{2}^{n-1}}$.
故答案为:$\frac{3a}{{2}^{n-1}}$.
点评 本题考查了等边三角形的性质、三角形中位线定理.三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
19.下列图形中,∠1与∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
14.下列调查,合适采用全面调查方式的是( )
| A. | 检测某型号手机的抗摔情况 | |
| B. | 了解某校七(1)班全体同学的身高情况 | |
| C. | 检测一批农产品的农药残留情况 | |
| D. | 检测某试验区水稻的株高生长情况 |
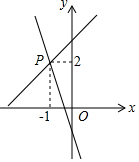 如图,己知直线y1=x+m与y2=kx-1相交于点P(-1,2),则关于x的不等式x+m<kx-1的解集在数轴上表示正确的是( )
如图,己知直线y1=x+m与y2=kx-1相交于点P(-1,2),则关于x的不等式x+m<kx-1的解集在数轴上表示正确的是( )

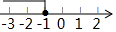
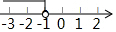
 如图,若AD是△ABC的高,AE是△ABC的角平分线,∠B=36°,∠ACD=66°,则∠AED=51°.
如图,若AD是△ABC的高,AE是△ABC的角平分线,∠B=36°,∠ACD=66°,则∠AED=51°.