题目内容
二次函数y=ax2＋bx﹣1（a≠0）的图象经过点（1，1），则a＋b＋1的值是
A. ﹣3 B. ﹣1 C. 2 D. 3
D
【解析】试题分析：根据二次函数图象上点的坐标特征，把（1，1）代入解析式可得到a+b﹣1=1，则a+b=2，所以a+b+1=3.
故选：D．
培优好卷单元加期末卷系列答案已知：如图，△ABC的∠B、∠C的平分线相交于点D，过D作MN∥BC交AB、AC分别于点M、N，求证：BM＋CN＝MN.
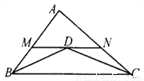
见解析
【解析】试题分析：根据角平分线的定义可得∠1=∠2，∠3=∠4，再根据两直线平行，内错角相等可得∠6=∠2，∠3=∠5，然后求出∠1=∠6，∠4=∠5，根据等角对等边的性质可得BM=DM，CN=DN，然后列式求解即可得证．
试题解析：证明：
∵BD、CF平分∠ABC、∠ACB，
∴∠1=∠2，∠3=∠4，
∵MN∥BC，
∴∠6=∠2，∠3=∠5，
... 将抛物线y=2（x﹣1）2+2向左平移3个单位，再向下平移4个单位，那么得到的抛物线的表达式为 ．
y=2﹣2
【解析】试题分析：按照“左加右减，上加下减”的规律可得抛物线y=2（x﹣1）2+2向左平移3个单位，再向下平移4个单位得到y=2（x﹣1+3）2+2﹣4=2（x+2）2﹣2．即可得抛物线的解析式为y=2（x+2）2﹣2． 如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸．A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元．
探究1：如果木板边长为1米，FC=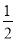
米，则一块木板用墙纸的费用需 元；
探究2：如果木板边长为2米，正方形EFCG的边长为x米，一块木板需用墙纸的费用为y元，
（1）用含x的代数式表示y（写过程）．
（2）如果一块木板需用墙纸的费用为225元，求正方形EFCG的边长为多少米？
（1）55，y=20x2﹣40x+240（2）正方形EFCG的边长为或米
【解析】【解析】
探究1：∵四边形ABCD是正方形，
∴AB=BC=CD=DA=1，
∴S正方形ABCD=1，
∵四边形EFCG是正方形，
∴EF=CF=，
∴S正方形EFCG=，BF=，
∴S△ABE==
∴空白部分的面积为：1﹣﹣=，
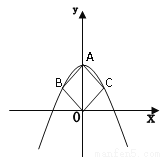
∴这块木板用墙纸的费用为：+8... 如图在平面直角坐标系中，二次函数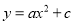
的图象过正方形ABOC的三个顶点A、B、C，则
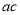值为__________。
-2
【解析】试题解析：设正方形的对角线OA长为2m，
则B（-m，m），C（m，m），A（0，2m）；
把A，C的坐标代入解析式可得：
c=2m①，am2+c=m②，
①代入②得：m2a+2m=m，解得：a=-，
则ac=-•2m=-2． 下列关于函数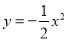
的图象说法：①图象是一条抛物线；②开口向下；③对称轴是y轴；④顶点（0，0），其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
D
【解析】
试题分析：函数是一种最基本的二次函数，画出图象，直接可知：
② 二次函数的图象是抛物线，正确；
②因为a=﹣＜0，抛物线开口向下，正确；
③因为b=0，对称轴是y轴，正确；
④顶点（0，0）也正确．
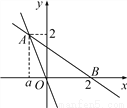
故选D． 如图，直线y＝－2x与直线y＝kx＋b相交于点A(a,2)，并且直线y＝kx＋b经过x轴上点B(2,0)．
(1)求直线y＝kx＋b的解析式；
(2)求两条直线与y轴围成的三角形面积；
(3)直接写出不等式(k＋2)x＋b≥0的解集．
（1）一次函数的解析式是y＝－x＋；（2）S△ABC＝；（3）x≥－1.
【解析】试题分析：利用代入法求出点A的坐标，然后根据待定系数法求出一次函数的解析式；
（2）根据图像求出交点C的坐标，然后可求三角形的面积；
（3）根据图像的位置求出不等式的解集.
试题解析：【解析】
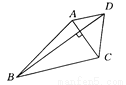
(1)把A(a,2)代入y＝－2x中，得－2a＝2，∴a＝－1，∴A(－1,2)，把A(－1,2)... 如图所示，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC＝5 ㎝， BD＝12 ㎝，则该梯形的两底之和等于____㎝．
13
【解析】【解析】
过点D作DE∥AC交BC的延长线于E，则DE与AC平行且相等，AD=CE．∵AC⊥BD，∴BD⊥DE．在Rt△BDE中，BE==13，∴BC+AD=13． 为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
(1) A型污水处理设备每周每台可以处理污水240 t,B型污水处理设备每周每台可以处理污水200 t(2)购买A型污水处理设备13台,购买B型污水处理设备7台时,所需资金最少,最少是226万元
【解析】（1）根据1台A型污水处理设备+2台B型污水处理设备=每周可以处理污水640吨，2台A型污水处理设备+3台B型污水处理设备=每周可以处理污水1080吨，关系式列出二元一次方程组，从而解答即可...