题目内容
如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.
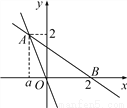
 (1)一次函数的解析式是y=-x+;(2)S△ABC=;(3)x≥-1.
【解析】试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:【解析】
(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)...
(1)一次函数的解析式是y=-x+;(2)S△ABC=;(3)x≥-1.
【解析】试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:【解析】
(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)...
如图,直线 、
、 、
、 表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
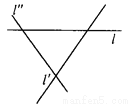
A. 一处 B. 二处 C. 三处 D. 四处
 D
【解析】如图所示,加油站站的地址有四处.
故选:D.
D
【解析】如图所示,加油站站的地址有四处.
故选:D. 如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
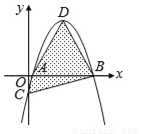
A. 1 B. 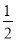 C.
C. 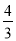 D.
D. 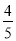
 D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D.
D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D. 二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则a+b+1的值是
A. ﹣3 B. ﹣1 C. 2 D. 3
 D
【解析】试题分析:根据二次函数图象上点的坐标特征,把(1,1)代入解析式可得到a+b﹣1=1,则a+b=2,所以a+b+1=3.
故选:D.
D
【解析】试题分析:根据二次函数图象上点的坐标特征,把(1,1)代入解析式可得到a+b﹣1=1,则a+b=2,所以a+b+1=3.
故选:D. 抛物线y=﹣(x+2)2﹣3的顶点坐标是( )
A. (2,﹣3) B. (﹣2,3) C. (2,3) D. (﹣2,﹣3)
 D
【解析】试题分析:∵抛物线y=﹣(x+2)2﹣3为抛物线解析式的顶点式,∴抛物线顶点坐标是(﹣2,﹣3).故选D.
D
【解析】试题分析:∵抛物线y=﹣(x+2)2﹣3为抛物线解析式的顶点式,∴抛物线顶点坐标是(﹣2,﹣3).故选D. 不等式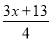 >
>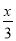 +2的解是_________.
+2的解是_________.
 x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3.
x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3. 如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24 ㎝,BC=26㎝,动点P从点A开始沿AD边以每秒1㎝的速度向D点运动,动点Q从点C开始沿CB边以每秒3㎝的速度向B运动,P,Q分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t s.

(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?
(3)t为何值时,四边形ABQP为矩形?
 (1)t=6时;(2)t=7时;(3)t=时.
【解析】试题分析:(1)要使四边形PQCD是平行四边形,则点在运动的过程中,只需PD=QC就满足题意;
(2)作DE⊥BC,PF⊥BC,垂足分别为E,F,要使四边形PQCD为等腰梯形,则QF=CE;依此即可求解;
(3)要使四边形ABQP为矩形,则点在运动的过程中,只需AP=BQ就满足题意.
试题解析:【解析】
由已知得AP...
(1)t=6时;(2)t=7时;(3)t=时.
【解析】试题分析:(1)要使四边形PQCD是平行四边形,则点在运动的过程中,只需PD=QC就满足题意;
(2)作DE⊥BC,PF⊥BC,垂足分别为E,F,要使四边形PQCD为等腰梯形,则QF=CE;依此即可求解;
(3)要使四边形ABQP为矩形,则点在运动的过程中,只需AP=BQ就满足题意.
试题解析:【解析】
由已知得AP... □ABCD的周长为36 cm,AB=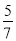 BC,则较长边的长为( )
BC,则较长边的长为( )
A. 15 cm B. 7.5 cm C. 21 cm D. 10.5 cm
 D
【解析】【解析】
∵?ABCD的周长=2(AB+BC)=36,∴AB+BC=18.∵AB=BC,∴BC=10.5.
故选D.
D
【解析】【解析】
∵?ABCD的周长=2(AB+BC)=36,∴AB+BC=18.∵AB=BC,∴BC=10.5.
故选D. 如果关于x的不等式(3m-1)x>3m-1的解集为x<1,那么m的取值范围是( )
A. m>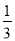 B. m<
B. m<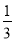 C. m>-
C. m>-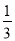 D. m<-
D. m<-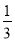
 B
【解析】根据一元一次不等式的解法和基本性质,可由关于x的不等式(3m-1)x>3m-1的解集为x<1,可知3m-1<0,解得m<.
故选:B.
B
【解析】根据一元一次不等式的解法和基本性质,可由关于x的不等式(3m-1)x>3m-1的解集为x<1,可知3m-1<0,解得m<.
故选:B. 
