题目内容
为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
(1) A型污水处理设备每周每台可以处理污水240 t,B型污水处理设备每周每台可以处理污水200 t(2)购买A型污水处理设备13台,购买B型污水处理设备7台时,所需资金最少,最少是226万元
【解析】（1）根据1台A型污水处理设备+2台B型污水处理设备=每周可以处理污水640吨，2台A型污水处理设备+3台B型污水处理设备=每周可以处理污水1080吨，关系式列出二元一次方程组，从而解答即可...
二次函数y=ax2＋bx﹣1（a≠0）的图象经过点（1，1），则a＋b＋1的值是
A. ﹣3 B. ﹣1 C. 2 D. 3
D
【解析】试题分析：根据二次函数图象上点的坐标特征，把（1，1）代入解析式可得到a+b﹣1=1，则a+b=2，所以a+b+1=3.
故选：D． □ABCD的周长为36 cm，AB=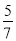
BC，则较长边的长为（ ）
A. 15 cm B. 7.5 cm C. 21 cm D. 10.5 cm
D
【解析】【解析】
∵?ABCD的周长=2（AB+BC）=36，∴AB+BC=18．∵AB=BC，∴BC=10.5．
故选D． 四边形ABCD中，AD//BC，AD＝BC，则四边形ABCD是_______四边形．
平行
【解析】【解析】
∵AD//BC，AD＝BC，∴四边形ABCD是平行四边形．故答案为：平行． 如图，平行四边形ABCD中，E，F分别为边AB，DC的中点，则图中共有平行四边形的个数是 （ ）
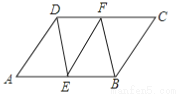
A. 3 B. 4 C. 5 D. 6
B
【解析】【解析】
∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．
∵E，F分别AB，CD的中点，∴AE=EB=DF=FC，∴四边形AEFD是平行四边形，四边形EFCB是平行四边形，四边形BEDF是平行四边形，∴平行四边形的个数共有4个．故选B． 不等式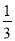
(x－m)＞3－m的解集为x＞1，则m的值为___.
x＞6
【解析】试题分析：去分母得，x﹣m＞3（3﹣m），
去括号得，x﹣m＞9﹣3m，
移项，合并同类项得，x＞9﹣2m。
∵此不等式的解集为x＞1，
∴9﹣2m=1，解得m=4。 如果关于x的不等式(3m－1)x＞3m－1的解集为x＜1，那么m的取值范围是( )
A. m＞
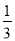B. m＜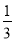
C. m＞－
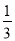D. m＜－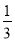
B
【解析】根据一元一次不等式的解法和基本性质，可由关于x的不等式(3m－1)x＞3m－1的解集为x＜1，可知3m-1＜0，解得m＜.
故选：B. （10分） 如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数．
360°．
【解析】试题分析：连接BE，根据三角形外角的性质可得∠1=∠C+∠D=∠CBE+∠DEB，再由四边形的内角和定理可得∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F=360°．
试题解析：【解析】
如图，连接BE．
∵∠1=∠C+∠D，∠1=∠CBE+∠DEB，
∴∠C+∠D=∠CB... 下列说法正确的是( )
A. “任意画一个三角形,其内角和为360°”是随机事件
B. 已知某篮球运动员投篮投中的概率为0.6,则他投10次可投中6次
C. 抽样调查选取样本时,所选样本可按自己的喜好选取
D. 检测某城市的空气质量,采用抽样调查法
D
【解析】试题解析：A、“任意画一个三角形，其内角和为360°”是不可能事件，故A错误；
B、已知某篮球运动员投篮投中的概率为0.6，则他投十次可能投中6次，故B错误；
C、抽样调查选取样本时，所选样本要具有广泛性、代表性，故C错误；
D、检测某城市的空气质量，采用抽样调查法，故D正确；
故选：D．