题目内容
将抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位,那么得到的抛物线的表达式为 .
 y=2﹣2
【解析】试题分析:按照“左加右减,上加下减”的规律可得抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位得到y=2(x﹣1+3)2+2﹣4=2(x+2)2﹣2.即可得抛物线的解析式为y=2(x+2)2﹣2.
y=2﹣2
【解析】试题分析:按照“左加右减,上加下减”的规律可得抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位得到y=2(x﹣1+3)2+2﹣4=2(x+2)2﹣2.即可得抛物线的解析式为y=2(x+2)2﹣2.
练习册系列答案
相关题目
若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是__.
 0或1
【解析】需要分类讨论:①若m=0,则函数为一次函数;②若m≠0,则函数为二次函数,由抛物线与x轴只有一个交点,得到根的判别式的值等于0,且m不为0,即可求出m的值.
【解析】
①若m=0,则函数y=2x+1,是一次函数,与x轴只有一个交点;
②若m≠0,则函数y=mx2+2x+1,是二次函数.
根据题意得:△=4﹣4m=0,
解得:m=1.
所以当m的...
0或1
【解析】需要分类讨论:①若m=0,则函数为一次函数;②若m≠0,则函数为二次函数,由抛物线与x轴只有一个交点,得到根的判别式的值等于0,且m不为0,即可求出m的值.
【解析】
①若m=0,则函数y=2x+1,是一次函数,与x轴只有一个交点;
②若m≠0,则函数y=mx2+2x+1,是二次函数.
根据题意得:△=4﹣4m=0,
解得:m=1.
所以当m的... 如图,直线 、
、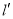 、
、 表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
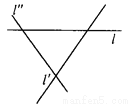
A. 一处 B. 二处 C. 三处 D. 四处
 D
【解析】如图所示,加油站站的地址有四处.
故选:D.
D
【解析】如图所示,加油站站的地址有四处.
故选:D. 已知a,b,c为△ABC三边长,且满足a2c2-b2c2=a4-b4,则它的形状为( )
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形
 D
【解析】试题分析:由a2c2-b2c2=a4-b4,得
a4+b2c2-a2c2-b4=(a4-b4)+(b2c2-a2c2)=(a2+b2)(a2-b2)-c2(a2-b2)=(a2-b2)(a2+b2-c2)=(a+b)(a-b)(a2+b2-c2)=0,
∵a+b>0,∴a-b=0或a2+b2-c2=0,
即a=b或a2+b2=c2,则△ABC为等腰三角形或直角三...
D
【解析】试题分析:由a2c2-b2c2=a4-b4,得
a4+b2c2-a2c2-b4=(a4-b4)+(b2c2-a2c2)=(a2+b2)(a2-b2)-c2(a2-b2)=(a2-b2)(a2+b2-c2)=(a+b)(a-b)(a2+b2-c2)=0,
∵a+b>0,∴a-b=0或a2+b2-c2=0,
即a=b或a2+b2=c2,则△ABC为等腰三角形或直角三... 广东特产专卖店销售龙眼干,其进价为每斤40元,按每斤60元出售,平均每天可售出100斤,后来经调查发现,单价每降低2元,则平均每天的销售量增加20斤.每斤降价多少元,每天销售额最大?
 20元
【解析】
试题分析:根据题意可以列出销售额与销售单价之间的关系式,然后整理为顶点式,即可解答本题.
【解析】
设每斤降价x元,销售额为y元,
y=(60﹣x)(100+)=﹣10(x﹣25)2+12250,
∴当x<25时,y随x的增大而增大,
∵60﹣40=20,
∴0≤x≤20,
∴当x=20时,y取得最大值,
即每斤降价20元时...
20元
【解析】
试题分析:根据题意可以列出销售额与销售单价之间的关系式,然后整理为顶点式,即可解答本题.
【解析】
设每斤降价x元,销售额为y元,
y=(60﹣x)(100+)=﹣10(x﹣25)2+12250,
∴当x<25时,y随x的增大而增大,
∵60﹣40=20,
∴0≤x≤20,
∴当x=20时,y取得最大值,
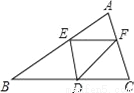
即每斤降价20元时... 已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为( )
A. 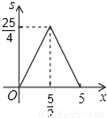 B.
B. 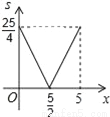 C.
C. 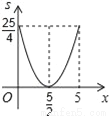 D.
D. 
 D
【解析】试题分析:∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,
∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),
纵观各选项,只有D选项图象符合.
故选D.
D
【解析】试题分析:∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,
∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),
纵观各选项,只有D选项图象符合.
故选D. 如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
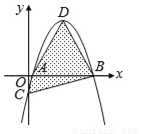
A. 1 B. 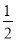 C.
C. 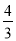 D.
D. 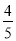
 D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D.
D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D. 二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则a+b+1的值是
A. ﹣3 B. ﹣1 C. 2 D. 3
 D
【解析】试题分析:根据二次函数图象上点的坐标特征,把(1,1)代入解析式可得到a+b﹣1=1,则a+b=2,所以a+b+1=3.
故选:D.
D
【解析】试题分析:根据二次函数图象上点的坐标特征,把(1,1)代入解析式可得到a+b﹣1=1,则a+b=2,所以a+b+1=3.
故选:D. □ABCD的周长为36 cm,AB=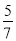 BC,则较长边的长为( )
BC,则较长边的长为( )
A. 15 cm B. 7.5 cm C. 21 cm D. 10.5 cm
 D
【解析】【解析】
∵?ABCD的周长=2(AB+BC)=36,∴AB+BC=18.∵AB=BC,∴BC=10.5.
故选D.
D
【解析】【解析】
∵?ABCD的周长=2(AB+BC)=36,∴AB+BC=18.∵AB=BC,∴BC=10.5.
故选D. 
