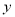题目内容
如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元.
探究1:如果木板边长为1米,FC=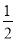 米,则一块木板用墙纸的费用需 元;
米,则一块木板用墙纸的费用需 元;
探究2:如果木板边长为2米,正方形EFCG的边长为x米,一块木板需用墙纸的费用为y元,

(1)用含x的代数式表示y(写过程).
(2)如果一块木板需用墙纸的费用为225元,求正方形EFCG的边长为多少米?
 (1)55,y=20x2﹣40x+240(2)正方形EFCG的边长为或米
【解析】【解析】
探究1:∵四边形ABCD是正方形,
∴AB=BC=CD=DA=1,
∴S正方形ABCD=1,
∵四边形EFCG是正方形,
∴EF=CF=,
∴S正方形EFCG=,BF=,
∴S△ABE==
∴空白部分的面积为:1﹣﹣=,
∴这块木板用墙纸的费用为:+8...
(1)55,y=20x2﹣40x+240(2)正方形EFCG的边长为或米
【解析】【解析】
探究1:∵四边形ABCD是正方形,
∴AB=BC=CD=DA=1,
∴S正方形ABCD=1,
∵四边形EFCG是正方形,
∴EF=CF=,
∴S正方形EFCG=,BF=,
∴S△ABE==
∴空白部分的面积为:1﹣﹣=,
∴这块木板用墙纸的费用为:+8...
 能考试期末冲刺卷系列答案
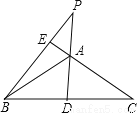
能考试期末冲刺卷系列答案如图,在等腰三角形ABC中,AD、BE分别是底边BC和腰AC上的高线,DA、BE的延长线交于点P.若∠BAC=110°,求∠P的度数。
 35°
【解析】试题分析:根据等腰三角形三线合一的性质可求得∠DAC的度数,根据对顶角相等求得∠EAP的度数,再由直角三角形的两锐角互余即可求得∠P的度数.
试题解析:
∵△ABC是等腰三角形,AB=AC,AD⊥BC,∠BAC=110°,
∴∠DAB=∠DAC=55°,
∵∠DAC=∠EAP(对顶角相等),
∴∠EAP=∠DAC=55°,
又∵BE是腰AC...
35°
【解析】试题分析:根据等腰三角形三线合一的性质可求得∠DAC的度数,根据对顶角相等求得∠EAP的度数,再由直角三角形的两锐角互余即可求得∠P的度数.
试题解析:
∵△ABC是等腰三角形,AB=AC,AD⊥BC,∠BAC=110°,
∴∠DAB=∠DAC=55°,
∵∠DAC=∠EAP(对顶角相等),
∴∠EAP=∠DAC=55°,
又∵BE是腰AC... 已知a,b,c为△ABC三边长,且满足a2c2-b2c2=a4-b4,则它的形状为( )
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形
 D
【解析】试题分析:由a2c2-b2c2=a4-b4,得
a4+b2c2-a2c2-b4=(a4-b4)+(b2c2-a2c2)=(a2+b2)(a2-b2)-c2(a2-b2)=(a2-b2)(a2+b2-c2)=(a+b)(a-b)(a2+b2-c2)=0,
∵a+b>0,∴a-b=0或a2+b2-c2=0,
即a=b或a2+b2=c2,则△ABC为等腰三角形或直角三...
D
【解析】试题分析:由a2c2-b2c2=a4-b4,得
a4+b2c2-a2c2-b4=(a4-b4)+(b2c2-a2c2)=(a2+b2)(a2-b2)-c2(a2-b2)=(a2-b2)(a2+b2-c2)=(a+b)(a-b)(a2+b2-c2)=0,
∵a+b>0,∴a-b=0或a2+b2-c2=0,
即a=b或a2+b2=c2,则△ABC为等腰三角形或直角三... 已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为( )
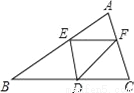
A. 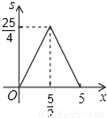 B.
B. 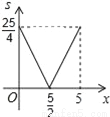 C.
C. 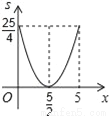 D.
D. 
 D
【解析】试题分析:∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,
∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),
纵观各选项,只有D选项图象符合.
故选D.
D
【解析】试题分析:∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,
∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),
纵观各选项,只有D选项图象符合.
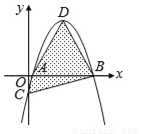
故选D. 如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
A. 1 B. 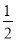 C.
C. 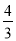 D.
D. 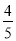
 D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D.
D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D. 二次函数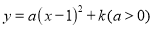 中
中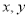 的几组对应值如下表.
的几组对应值如下表.
| -2 | 1 | 5 |
| m | n | p |
表中m、n、p的大小关系为________________(用“<”连接)
 n<m<p
【解析】【解析】
设(-2,m)关于对称轴的对称点为(x,m).∵二次函数的对称轴为x=1,∴ ,解得:x=4.∵a>0,∴抛物线开口向上,在对称轴右侧,y随x的增大而增大.∵1<4<5,∴n<m<p.故答案为:n<m<p.
n<m<p
【解析】【解析】
设(-2,m)关于对称轴的对称点为(x,m).∵二次函数的对称轴为x=1,∴ ,解得:x=4.∵a>0,∴抛物线开口向上,在对称轴右侧,y随x的增大而增大.∵1<4<5,∴n<m<p.故答案为:n<m<p. 二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则a+b+1的值是
A. ﹣3 B. ﹣1 C. 2 D. 3
 D
【解析】试题分析:根据二次函数图象上点的坐标特征,把(1,1)代入解析式可得到a+b﹣1=1,则a+b=2,所以a+b+1=3.
故选:D.
D
【解析】试题分析:根据二次函数图象上点的坐标特征,把(1,1)代入解析式可得到a+b﹣1=1,则a+b=2,所以a+b+1=3.
故选:D. 不等式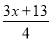 >
>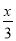 +2的解是_________.
+2的解是_________.
 x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3.
x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3. 四边形ABCD中,AD//BC,AD=BC,则四边形ABCD是_______四边形.
 平行
【解析】【解析】
∵AD//BC,AD=BC,∴四边形ABCD是平行四边形.故答案为:平行.
平行
【解析】【解析】
∵AD//BC,AD=BC,∴四边形ABCD是平行四边形.故答案为:平行.