题目内容
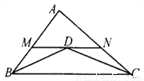
已知：如图，△ABC的∠B、∠C的平分线相交于点D，过D作MN∥BC交AB、AC分别于点M、N，求证：BM＋CN＝MN.
见解析
【解析】试题分析：根据角平分线的定义可得∠1=∠2，∠3=∠4，再根据两直线平行，内错角相等可得∠6=∠2，∠3=∠5，然后求出∠1=∠6，∠4=∠5，根据等角对等边的性质可得BM=DM，CN=DN，然后列式求解即可得证．
试题解析：证明：
∵BD、CF平分∠ABC、∠ACB，
∴∠1=∠2，∠3=∠4，
∵MN∥BC，
∴∠6=∠2，∠3=∠5，
...
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
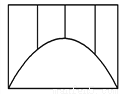
如图，一座抛物线型拱桥，桥下水面宽度是4m时，拱高为2m，一艘木船宽2m.要能顺利从桥下通过，船顶点与桥拱之间的间隔应不少于0.3m，那么木船的高不得超过 ______m.
1.2
【解析】以水面所在水平线为x轴，过拱桥顶点作水平线的垂线，作为y轴，建立坐标系，设水平面与拱桥的交点为A（-2，0），B（2，0），C（0，2），利用待定系数法设函数的解析式为y=a（x+2）（x-2）代入点C坐标，求得a=-，即抛物线的解析式为y=-（x+2）（x-2），令x=1，解得y=1.5，船顶与桥拱之间的间隔应不少于0.3，则木船的最高高度为1.5-0.3=1.2米.
... 若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是__．
0或1
【解析】需要分类讨论：①若m=0，则函数为一次函数；②若m≠0，则函数为二次函数，由抛物线与x轴只有一个交点，得到根的判别式的值等于0，且m不为0，即可求出m的值．
【解析】
①若m=0，则函数y=2x+1，是一次函数，与x轴只有一个交点；
②若m≠0，则函数y=mx2+2x+1，是二次函数．
根据题意得：△=4﹣4m=0，
解得：m=1．
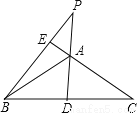
所以当m的... 如图，在等腰三角形ABC中，AD、BE分别是底边BC和腰AC上的高线，DA、BE的延长线交于点P．若∠BAC=110°，求∠P的度数。
35°
【解析】试题分析：根据等腰三角形三线合一的性质可求得∠DAC的度数，根据对顶角相等求得∠EAP的度数，再由直角三角形的两锐角互余即可求得∠P的度数.
试题解析：
∵△ABC是等腰三角形，AB=AC，AD⊥BC，∠BAC=110°，
∴∠DAB=∠DAC=55°，
∵∠DAC=∠EAP（对顶角相等），
∴∠EAP=∠DAC=55°，
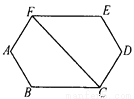
又∵BE是腰AC... 已知：如图，AB＝DE，CD＝FA，∠A＝∠D，∠AFC＝∠DCF，则BC＝EF．你能说出它们相等的理由吗?
见解析
【解析】试题分析：首先连接CE、BF，然后根据条件可证明△ABF≌△DEC，再根据全等三角形的性质可得∠3=∠4，BF=EC，然后证明△BCF≌△EFC可得BC=EF．
试题解析：连接CE、BF，如图：
在△ABF和△DEC中， ，
∴△ABF≌△DEC(SAS)，
∴∠3=∠4，BF=EC，
∵∠AFC=∠DCF，
∴∠AFC?∠3=∠DCF?∠... 三角形的一边上有一点，它到三个顶点的距离相等，则这个三角形是_______三角形．
直角
【解析】∵直角三角形斜边上的中线等于斜边的一半，
∴这个三角形是直角三角形.
故答案为：直角. 如图，直线
、
、
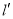表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有( )
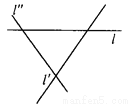
A. 一处 B. 二处 C. 三处 D. 四处
D
【解析】如图所示，加油站站的地址有四处.
故选：D. 已知a,b,c为△ABC三边长,且满足a2c2－b2c2=a4－b4，则它的形状为( )
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形
D
【解析】试题分析：由a2c2-b2c2=a4-b4，得
a4+b2c2-a2c2-b4=（a4-b4）+（b2c2-a2c2）=（a2+b2）（a2-b2）-c2（a2-b2）=（a2-b2）（a2+b2-c2）=（a+b）（a-b）（a2+b2-c2）=0，
∵a+b＞0，∴a-b=0或a2+b2-c2=0，
即a=b或a2+b2=c2，则△ABC为等腰三角形或直角三... 二次函数y=ax2＋bx﹣1（a≠0）的图象经过点（1，1），则a＋b＋1的值是
A. ﹣3 B. ﹣1 C. 2 D. 3
D
【解析】试题分析：根据二次函数图象上点的坐标特征，把（1，1）代入解析式可得到a+b﹣1=1，则a+b=2，所以a+b+1=3.
故选：D．