题目内容
10.如图1,在平面直角坐标系中,点A,B的坐标分别为A(m,0),B(n,0)且m、n满足|m+2|+$\sqrt{5-n}$=0,现同时将点A,B分别向上平移3个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.(1)求点C,D的坐标及四边形OBDC的面积;
(2)如图2,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)$\frac{∠DCP+∠BOP}{∠CPO}$的值是否发生变化,并说明理由..
(3)在四边形OBDC内是否存在一点P,连接PO,PB,PC,PD,使S△PCD=S△PBD;S△POB:S△POC=5:6,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
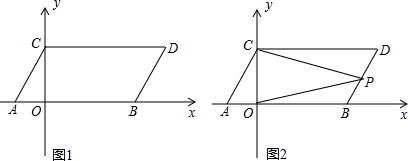
分析 (1)根据非负数的性质得到m=-2,n=5,求得A(-2,0),B(5,0),根据平移的性质得到点C(0,3),D(7,3);即可得到结果;
(2)过点P作PE∥CD,根据两直线平行,内错角相等可得∠DCP=∠CPE,根据平行公理可得PE∥AB,再根据两直线平行,内错角相等可得∠BOP=∠OPE,然后求出∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,再求出比值即可;
(3)如图3,过P作PM⊥OB于M,并反向延长交CD于N,设P(m,n),根据S△POB:S△POC=5:6,于是得到$\frac{1}{2}$×5•n=$\frac{1}{2}×3•m$,求得m=$\frac{5}{3}$n,①由于S△PCD=S△PBD,于是得到$\frac{1}{2}$×7•(3-n)=$\frac{1}{2}$(5-m+7-m)×3-$\frac{1}{2}$(5-m)n-$\frac{1}{2}$(7-m)(3-n),②解方程组即可得到结论.
解答 解:(1)∵|m+2|+$\sqrt{5-n}$=0,
∴m=-2,n=5,
∴A(-2,0),B(5,0),
∵点A,B分别向上平移3个单位,再向右平移2个单位,
∴点C(0,3),D(7,3);
∵OB=5,
∴S四边形OBDC=$\frac{1}{2}$(5+7)×3=18;
(2)$\frac{∠DCP+∠BOP}{∠CPO}$=1,比值不变.
理由如下:由平移的性质可得AB∥CD,
如图,过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
∴$\frac{∠DCP+∠BOP}{∠CPO}$=1,比值不变;
(3)存在,
如图3,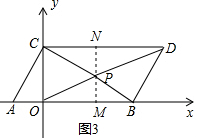 过P作PM⊥OB于M,并反向延长交CD于N,
过P作PM⊥OB于M,并反向延长交CD于N,
∵CD∥OB,
∴PN⊥CD,
设P(m,n),
∵S△POB:S△POC=5:6,
∴$\frac{1}{2}$×5•n=$\frac{1}{2}×3•m$,
∴m=$\frac{5}{3}$n,①
∵S△PCD=S△PBD,
∴$\frac{1}{2}$×7•(3-n)=$\frac{1}{2}$(5-m+7-m)×3-$\frac{1}{2}$(5-m)n-$\frac{1}{2}$(7-m)(3-n),
化简得-3m+9n=6②,
把①代入②,解得:m=4,n=2,
∴P(4,2).
∴存在这样一点P,使S△PCD=S△PBD;S△POB:S△POC=5:6.
点评 本题考查了坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移,熟记各性质是解题的关键.

| A. | 4-2a | B. | 0 | C. | 2a-4 | D. | 4 |
 如图,DE∥BC,AD:DB=2:3,EC=6,则AE的长是4.
如图,DE∥BC,AD:DB=2:3,EC=6,则AE的长是4.