题目内容

19．已知方程$\left\{{\begin{array}{l}{3x+2y-z=0}\\{6x+3y+2z=0}\end{array}$，则x：y：z=-7：12：3．

分析 把z看成已知数，解关于x、y的方程组，求出x、y的值，再代入求出即可．

解答 解：原方程组化为：$\left\{\begin{array}{l}{3x+2y=z①}\\{6x+3y=-2z②}\end{array}\right.$
①×2-②得：y=4z，
把y=4z代入①得：3x+8z=z，
解得：x=-$\frac{7}{3}$z，
所以x：y：z=-$\frac{7}{3}$z：4z：z=-7：12：3，
故答案为：-7：12：3．

点评 本题考查了解三元一次方程组的应用，能求出x、y的值是解此题的关键，难度不是很大．

练习册系列答案
相关题目
11．用配方法解下列方程：
（1）x2+12x-15=0；
（2）3x2-5x=2；
（3）$\frac{1}{4}$x2-x-4=0．
10．如图1，在平面直角坐标系中，点A，B的坐标分别为A（m，0），B（n，0）且m、n满足|m+2|+$\sqrt{5-n}$=0，现同时将点A，B分别向上平移3个单位，再向右平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
（1）求点C，D的坐标及四边形OBDC的面积；
（2）如图2，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）$\frac{∠DCP+∠BOP}{∠CPO}$的值是否发生变化，并说明理由．．
（3）在四边形OBDC内是否存在一点P，连接PO，PB，PC，PD，使S△PCD=S△PBD；S△POB：S△POC=5：6，若存在这样一点，求出点P的坐标，若不存在，试说明理由． 
7．下列事件中，必然事件是（　　）
A．打开电视机，正在播巴西世界杯新闻
B．下雨后，天空出现彩虹
C．随机掷一枚硬币，落地后正面朝上
D．3个人分成两组，一定有2个人分在一组
14．计算
（1）6tan230°-cos30°•tan60°-2sin45°+cos60°．
（2）$\sqrt{2}$（2cos45°-sin60°）+$\frac{\sqrt{24}}{4}$．
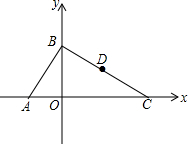4．如图，在平面直角坐标系中，点O为坐标原点，直线y=$\sqrt{3}$x+2$\sqrt{3}$与x轴、y轴分布交于A、B两点，过点B作AB的垂线，交x轴于点C，点D为BC中点．
（1）求点D的坐标；
（2）动点P从B出发沿BA向点A运动，速度为$\sqrt{3}$个单位/秒，动点Q从D出发沿DB向点B运动，速度为1个单位/秒，两点同时出发，并且当一个点到达终点时另一个点也同时停止运动，连接PQ，将线段PQ绕点Q顺时针旋转60°得到线段P′Q的垂线，垂足为E，连接BE，设点P运动时间为t秒，线段BE的长为d（d≠0），求d与t之间的函数关系式（直接写出t的取值范围）；
（3）在（2）的条件下，连接AE、DE、AD，当t为何值时，△ADE为直角三角形．
11．若$\sqrt{12m}$是整数，则正整数m的最小值是（　　）
A．3B．4C．5D．6
8．化简分数：$\frac{5}{-36}$=-$\frac{5}{36}$，-$\frac{-6}{7}$=$\frac{6}{7}$．
9．解方程：
（1）$\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3
（2）$\frac{x-2}{x+2}$-$\frac{16}{{x}^{2}-4}$=$\frac{x+2}{x-2}$
（3）x2-9=0
（4）x2+4x-5=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网