题目内容
11.已知x=$\frac{1}{2}$($\sqrt{7}$+$\sqrt{5}$),y=$\frac{1}{2}$($\sqrt{7}$-$\sqrt{5}$),则x2-xy+y2=5$\frac{1}{2}$.分析 所求的式子可以化成(x-y)2+xy,然后代入求解即可.
解答 解:原式=(x-y)2+xy=5+$\frac{1}{4}$×2=5$\frac{1}{2}$.
故答案是:5$\frac{1}{2}$.
点评 本题考查二次根式的求值,正确对所求的式子进行变形是关键.

练习册系列答案
相关题目
16.下列各式计算正确的是( )
| A. | $\sqrt{{2}^{2}+{3}^{2}}$=2+3 | B. | 3$\sqrt{2}$+5$\sqrt{3}$=8$\sqrt{6}$ | ||
| C. | $\sqrt{1{5}^{2}-1{2}^{2}}$=$\sqrt{15+12}$×$\sqrt{15-12}$ | D. | $\sqrt{4\frac{1}{2}}$=2$\sqrt{\frac{1}{2}}$ |
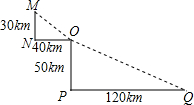 如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是5000万元/km,该沿江高速公路的造价预计是多少?
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是5000万元/km,该沿江高速公路的造价预计是多少?